Find Gcf Of 9 And 12 In Simple Steps

Quick Links :

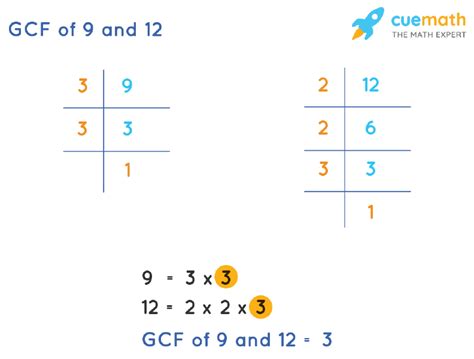
Finding the greatest common factor (GCF) of two numbers is a simple process that can be done in a few steps. In this case, we want to find the GCF of 9 and 12.

What is the Greatest Common Factor (GCF)?

The greatest common factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. In other words, it is the largest number that is a factor of both numbers.

Step 1: List the Factors of Each Number

To find the GCF of 9 and 12, we need to list the factors of each number.

Factors of 9: 1, 3, 9 Factors of 12: 1, 2, 3, 4, 6, 12

Step 2: Identify the Common Factors

Next, we need to identify the common factors of 9 and 12. The common factors are the numbers that appear in both lists.

Common factors: 1, 3

Step 3: Find the Greatest Common Factor

Finally, we need to find the greatest common factor. The greatest common factor is the largest number in the list of common factors.

GCF of 9 and 12: 3

Example Problems

Here are a few example problems to help you practice finding the GCF:

• Find the GCF of 6 and 8:
  • Factors of 6: 1, 2, 3, 6
  • Factors of 8: 1, 2, 4, 8
  • Common factors: 1, 2
  • GCF: 2
• Find the GCF of 15 and 20:
  • Factors of 15: 1, 3, 5, 15
  • Factors of 20: 1, 2, 4, 5, 10, 20
  • Common factors: 1, 5
  • GCF: 5

Conclusion

Finding the greatest common factor (GCF) of two numbers is a simple process that involves listing the factors of each number, identifying the common factors, and finding the greatest common factor. With practice, you can become proficient in finding the GCF of two numbers.