Every Parallel Is A Square

Quick Links :

In the world of geometry, shapes and figures are a fundamental part of understanding the world around us. Among these shapes, the concept of squares and rectangles has been widely studied and utilized in various fields. However, have you ever stopped to think about the relationship between squares and parallelograms? Specifically, the concept that every parallelogram is a square? In this article, we'll delve into the world of geometry and explore this idea.

Geometry, the branch of mathematics that deals with the study of shapes, sizes, and positions of objects, has been a cornerstone of human understanding for centuries. From the ancient Greeks to modern-day mathematicians, the study of geometry has led to numerous breakthroughs in various fields, including architecture, engineering, and physics. One of the most basic yet essential concepts in geometry is the study of two-dimensional shapes, including squares, rectangles, and parallelograms.

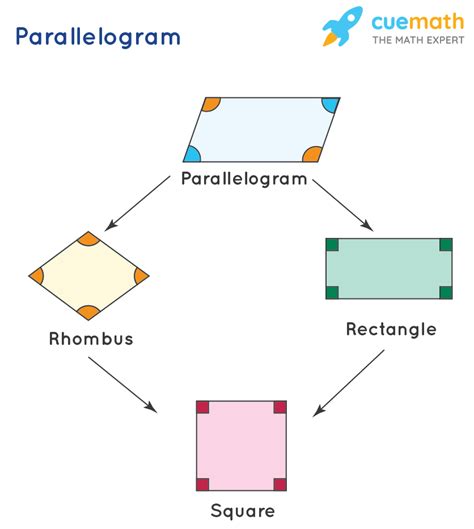
What is a Parallelogram?

A parallelogram is a type of quadrilateral, a four-sided shape, where opposite sides are parallel and equal in length. The opposite angles of a parallelogram are also equal, making it a unique shape with distinct properties. Parallelograms are commonly found in architecture, where they are used to create stable and balanced structures.

What is a Square?

A square, on the other hand, is a type of quadrilateral where all four sides are equal in length, and all four angles are right angles (90 degrees). Squares are a special type of rectangle, where the length and width are equal. Squares are commonly used in design and architecture, where symmetry and balance are crucial.

The Relationship Between Parallelograms and Squares

Now that we've established what parallelograms and squares are, let's explore the relationship between them. As it turns out, every parallelogram can be transformed into a square by applying a series of geometric transformations. This concept is based on the idea that a parallelogram can be divided into two congruent triangles, which can then be rearranged to form a square.

Proof by Construction

To demonstrate this concept, let's construct a parallelogram and transform it into a square step by step.

1. Start with a parallelogram ABCD, where AB is parallel to CD, and AD is parallel to BC.
2. Draw a diagonal AC, which divides the parallelogram into two congruent triangles, ABC and ADC.
3. Rearrange the two triangles to form a new quadrilateral, where the vertices of the triangles are connected in a different order.
4. By rearranging the triangles, we can see that the new quadrilateral has four equal sides and four right angles, making it a square.

This construction demonstrates that every parallelogram can be transformed into a square by rearranging its constituent triangles.

Practical Applications

So, why is this concept important? The relationship between parallelograms and squares has numerous practical applications in various fields, including:

• Architecture: Understanding the relationship between parallelograms and squares is crucial in designing stable and balanced structures.
• Engineering: The concept of transforming parallelograms into squares is used in computer-aided design (CAD) software to create precise and accurate models.
• Physics: The study of geometric transformations is essential in understanding the behavior of objects in motion.

Conclusion

In conclusion, the concept that every parallelogram is a square is a fundamental idea in geometry, with far-reaching implications in various fields. By understanding the relationship between these two shapes, we can unlock new insights and applications in architecture, engineering, and physics. Whether you're a mathematician, scientist, or simply a curious learner, the world of geometry is full of fascinating concepts and ideas waiting to be explored.