In today's increasingly complex and interconnected world, discrete mathematics plays a vital role in various aspects of our daily lives. From the simplest tasks to the most complex systems, discrete mathematics provides the underlying framework for understanding and analyzing problems. In this article, we will explore seven ways discrete mathematics applies to real life, highlighting its significance and impact on our world.
Discrete mathematics is a branch of mathematics that deals with mathematical structures that are fundamentally discrete, meaning they are made up of individual, distinct elements rather than continuous values. This branch of mathematics has numerous applications in computer science, information technology, engineering, economics, and many other fields.

1. Computer Networking and Cybersecurity
Discrete mathematics is essential in computer networking and cybersecurity. Graph theory, a fundamental area of discrete mathematics, is used to model and analyze network structures, ensuring efficient data transmission and communication. Network administrators use graph theory to design and optimize network topologies, guaranteeing that data packets are routed efficiently and securely.
In cybersecurity, discrete mathematics is used to develop secure encryption algorithms, such as RSA and elliptic curve cryptography, which rely on number theory and algebraic geometry. These algorithms protect online transactions and communication, safeguarding sensitive information from unauthorized access.

Key Concepts:
- Graph theory
- Number theory
- Algebraic geometry
- Encryption algorithms
2. Data Analysis and Machine Learning
Discrete mathematics is crucial in data analysis and machine learning. Combinatorics, another area of discrete mathematics, is used to analyze and interpret large datasets, identifying patterns and relationships. Machine learning algorithms, such as decision trees and clustering, rely on combinatorial techniques to classify and group data.
In data analysis, discrete mathematics is used to develop statistical models, such as probability theory and statistical inference, which help analyze and interpret data. These models enable data analysts to make informed decisions, identify trends, and predict future outcomes.
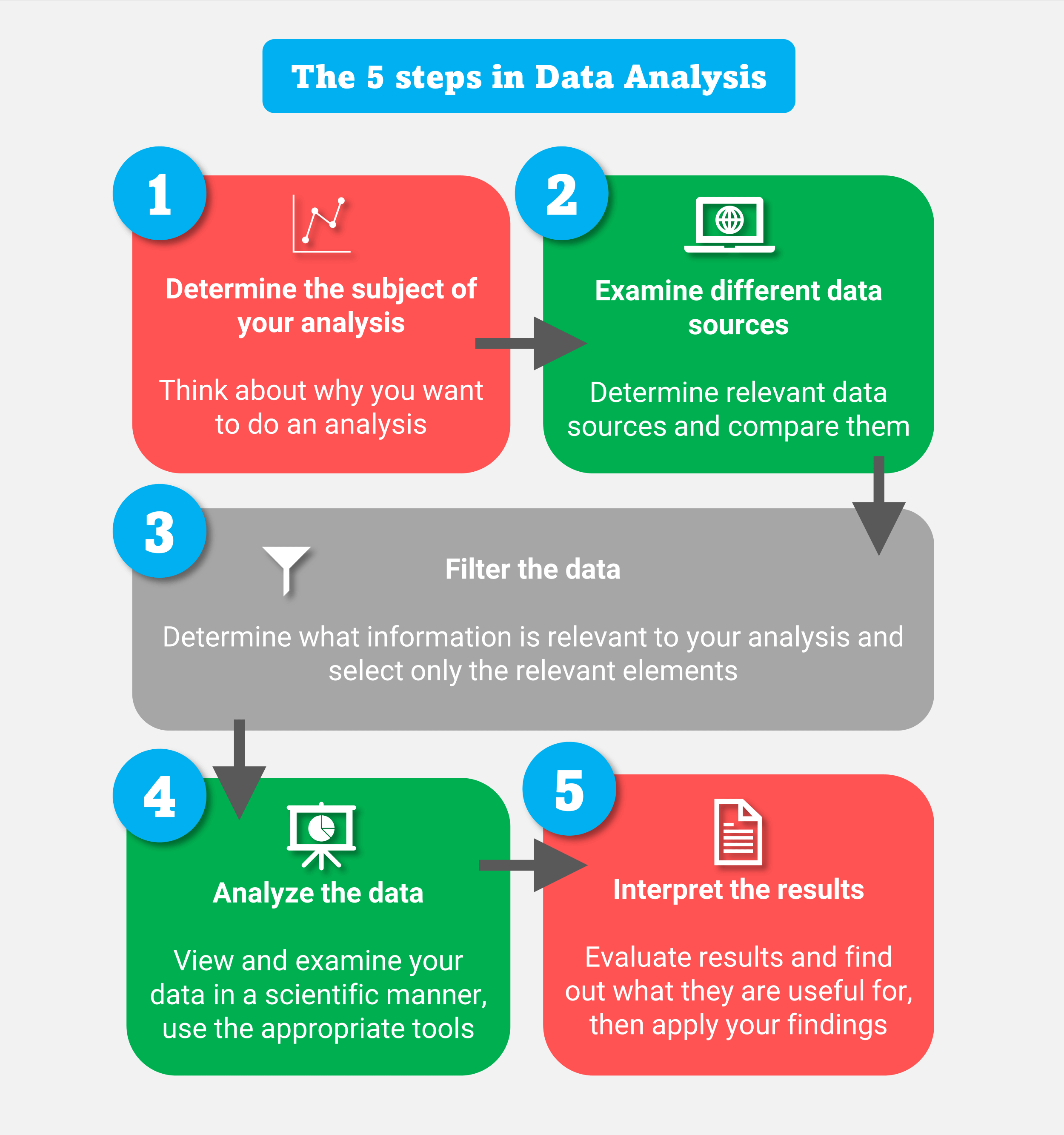
Key Concepts:
- Combinatorics
- Probability theory
- Statistical inference
- Machine learning algorithms
3. Optimization and Logistics
Discrete mathematics is applied in optimization and logistics to solve complex problems. Linear programming, a technique used to optimize linear objective functions, relies on discrete mathematics to find the best solution. This technique is used in logistics to optimize routes, schedules, and resource allocation.
In supply chain management, discrete mathematics is used to develop models that predict demand, manage inventory, and optimize production. These models help companies reduce costs, improve efficiency, and increase customer satisfaction.

Key Concepts:
- Linear programming
- Optimization techniques
- Supply chain management
- Logistics
4. Coding Theory and Error Detection
Discrete mathematics is used in coding theory to develop error-detecting and error-correcting codes. These codes are essential in digital communication, ensuring that data is transmitted accurately and reliably.
In coding theory, discrete mathematics is used to develop algorithms that detect and correct errors, guaranteeing that data is transmitted correctly. This is critical in applications such as satellite communication, where data transmission is prone to errors.

Key Concepts:
- Coding theory
- Error-detecting codes
- Error-correcting codes
- Digital communication
5. Computer Vision and Image Processing
Discrete mathematics is applied in computer vision and image processing to analyze and interpret visual data. Graph theory is used to model and analyze image structures, enabling computers to recognize patterns and objects.
In computer vision, discrete mathematics is used to develop algorithms that detect edges, recognize shapes, and track objects. These algorithms are critical in applications such as self-driving cars, medical imaging, and surveillance systems.

Key Concepts:
- Graph theory
- Image processing
- Computer vision
- Object recognition
6. Economics and Finance
Discrete mathematics is used in economics and finance to model and analyze complex systems. Game theory, a branch of discrete mathematics, is used to study strategic decision-making, enabling economists to predict market behavior and optimize economic outcomes.
In finance, discrete mathematics is used to develop models that predict stock prices, manage risk, and optimize investment portfolios. These models help investors make informed decisions, reducing the risk of financial losses.

Key Concepts:
- Game theory
- Economic modeling
- Financial modeling
- Risk management
7. Social Network Analysis
Discrete mathematics is applied in social network analysis to study the structure and behavior of social networks. Graph theory is used to model and analyze social networks, enabling researchers to understand how information spreads, identify influential individuals, and predict social trends.
In social network analysis, discrete mathematics is used to develop algorithms that detect communities, predict relationships, and identify clusters. These algorithms help researchers understand social dynamics, enabling them to develop effective strategies for social change.

Key Concepts:
- Graph theory
- Social network analysis
- Community detection
- Relationship prediction






