Standard Normal Distribution Applications And Assignment Examples

Quick Links :

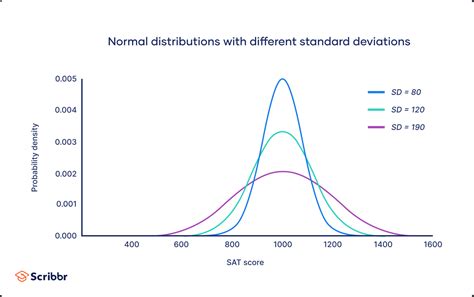
In statistics, the standard normal distribution, also known as the z-distribution, plays a crucial role in various applications. The standard normal distribution is a specific type of normal distribution where the mean is 0 and the standard deviation is 1. This distribution is widely used in statistical analysis, hypothesis testing, and data analysis.

The standard normal distribution has numerous applications in real-world scenarios, such as in finance, engineering, medicine, and social sciences. In this article, we will explore the applications of the standard normal distribution and provide assignment examples to help illustrate its uses.

Understanding the Standard Normal Distribution

The standard normal distribution is a continuous probability distribution that is symmetric about the mean, which is 0. The distribution is characterized by a bell-shaped curve, with the majority of the data points clustered around the mean and tapering off gradually towards the extremes.

The standard normal distribution is often denoted by the symbol Z and has a mean of 0 and a standard deviation of 1. The distribution is defined by the probability density function:

f(Z) = (1/√(2π)) * e^(-Z^2/2)

where Z is the random variable, π is the mathematical constant pi, and e is the base of the natural logarithm.

Applications of the Standard Normal Distribution

The standard normal distribution has numerous applications in various fields, including:

1. Finance: In finance, the standard normal distribution is used to model asset prices and returns. It is also used to estimate the probability of stock prices exceeding certain thresholds.
2. Engineering: In engineering, the standard normal distribution is used to model the variability of physical systems, such as the length of components or the strength of materials.
3. Medicine: In medicine, the standard normal distribution is used to model the distribution of medical test scores and to diagnose diseases.
4. Social Sciences: In social sciences, the standard normal distribution is used to model the distribution of attitudes and opinions.

Assignment Examples

Here are some assignment examples that illustrate the applications of the standard normal distribution:

Example 1: Finance

A financial analyst wants to estimate the probability that a stock will increase in value by more than 10% in the next quarter. Assuming that the stock prices follow a standard normal distribution with a mean of 0 and a standard deviation of 1, calculate the probability that the stock will increase in value by more than 10%.

Solution:

Let Z be the random variable representing the stock price increase. We want to find P(Z > 1.1), which is equivalent to finding P(Z > 1.1/1) = P(Z > 1.1).

Using a standard normal distribution table or calculator, we find that P(Z > 1.1) = 0.1357.

Therefore, the probability that the stock will increase in value by more than 10% is approximately 13.57%.

Example 2: Engineering

A manufacturing company produces components with lengths that follow a standard normal distribution with a mean of 10 cm and a standard deviation of 0.5 cm. Find the probability that a randomly selected component has a length greater than 10.5 cm.

Solution:

Let Z be the random variable representing the component length. We want to find P(Z > 10.5), which is equivalent to finding P((Z - 10)/0.5 > (10.5 - 10)/0.5) = P(Z > 2).

Using a standard normal distribution table or calculator, we find that P(Z > 2) = 0.0228.

Therefore, the probability that a randomly selected component has a length greater than 10.5 cm is approximately 2.28%.

Example 3: Medicine

A doctor wants to diagnose a patient with a disease based on the results of a medical test. The test scores follow a standard normal distribution with a mean of 0 and a standard deviation of 1. If the patient's test score is 1.5, what is the probability that the patient has the disease?

Solution:

Let Z be the random variable representing the test score. We want to find P(Z > 1.5), which is equivalent to finding P(Z > 1.5/1) = P(Z > 1.5).

Using a standard normal distribution table or calculator, we find that P(Z > 1.5) = 0.0668.

Therefore, the probability that the patient has the disease is approximately 6.68%.

Gallery of Standard Normal Distribution

Frequently Asked Questions

We hope this article has provided you with a comprehensive understanding of the standard normal distribution and its applications. Whether you're a student, researcher, or professional, the standard normal distribution is an essential tool to have in your statistical toolkit.