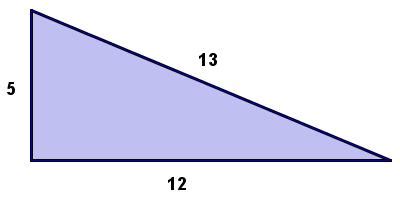
Triangles are one of the most fundamental shapes in geometry, and they have been studied for thousands of years. Within the realm of triangles, there exists a special category known as 5-12-13 triangles, which are right-angled triangles with side lengths of 5, 12, and 13 units. These triangles have some remarkable properties that have fascinated mathematicians and puzzle enthusiasts alike. In this article, we will delve into five surprising facts about 5-12-13 triangles that will leave you amazed.
Fact #1: The Pythagorean Connection

The 5-12-13 triangle is a Pythagorean triple, meaning that it satisfies the Pythagorean theorem, which states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is a fundamental concept in geometry and has numerous applications in various fields, including physics, engineering, and architecture.
Fact #2: The Ubiquity of 5-12-13 Triangles
Appearances in Real-World Applications

The 5-12-13 triangle appears in various real-world applications, such as construction, engineering, and design. For instance, the triangle can be used to construct a right-angled triangle with a hypotenuse of 13 units, which is a common requirement in building design. Additionally, the triangle's dimensions are often used in puzzles and brain teasers, making it a popular choice among puzzle enthusiasts.
Fact #3: The Geometric Mean
Unveiling the Hidden Pattern

The 5-12-13 triangle has a fascinating property related to the geometric mean. The geometric mean of two numbers is the square root of their product. In the case of the 5-12-13 triangle, the geometric mean of the two shorter sides (5 and 12) is equal to the length of the hypotenuse (13). This property is a result of the triangle's Pythagorean nature and has been exploited in various mathematical derivations.
Fact #4: The Triangular Number Sequence
A Connection to Number Theory

The 5-12-13 triangle has a surprising connection to the triangular number sequence. Triangular numbers are a sequence of numbers that can be represented as the sum of consecutive integers, starting from 1. The 5-12-13 triangle's side lengths form a triangular number sequence, with 5 being the 5th triangular number, 12 being the 6th triangular number, and 13 being the 7th triangular number. This connection highlights the intricate relationships between geometry and number theory.
Fact #5: The Puzzle Connection
A Favorite Among Puzzle Enthusiasts

The 5-12-13 triangle has been a favorite among puzzle enthusiasts for centuries. The triangle's dimensions have been used in various puzzles, such as the classic "Pythagorean puzzle," which requires the solver to find the length of the hypotenuse given the lengths of the other two sides. The 5-12-13 triangle's appearance in puzzles is a testament to its mathematical significance and aesthetic appeal.
Gallery of Triangular Wonders






FAQs
What is a Pythagorean triple?
+A Pythagorean triple is a set of three positive integers that satisfy the Pythagorean theorem, which states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
What are some real-world applications of the 5-12-13 triangle?
+The 5-12-13 triangle has numerous real-world applications, including construction, engineering, and design. It can be used to construct a right-angled triangle with a hypotenuse of 13 units, which is a common requirement in building design.
What is the geometric mean of two numbers?
+The geometric mean of two numbers is the square root of their product.
In conclusion, the 5-12-13 triangle is a fascinating mathematical object with numerous surprising properties and connections. From its Pythagorean nature to its appearances in real-world applications, puzzles, and number theory, this triangle is a true marvel of mathematics. We hope that this article has inspired you to explore the wonderful world of triangles and discover more of their secrets.