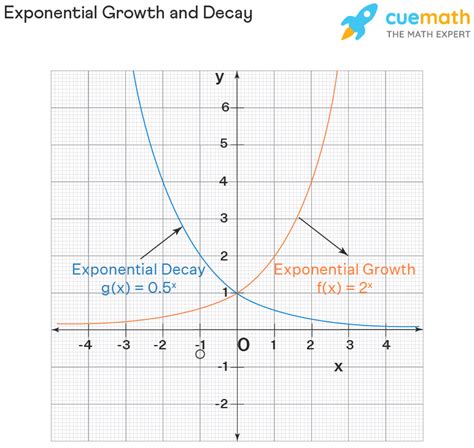
Exponential decay is a fundamental concept in mathematics, describing the process by which a quantity decreases exponentially over time. In graphs, exponential decay can be identified by specific features that help distinguish it from other types of decay. In this article, we will explore the 5 key graph features that indicate exponential decay.

Feature 1: Decreasing Trend The first feature of an exponential decay graph is a decreasing trend. As the input or x-value increases, the output or y-value decreases. This trend is characterized by a downward slope, indicating that the quantity is decreasing over time.
Feature 2: Non-Linear Relationship Exponential decay graphs exhibit a non-linear relationship between the input and output values. Unlike linear relationships, where the rate of change is constant, exponential decay graphs have a variable rate of change that decreases over time.

Feature 3: Asymptotic Behavior Exponential decay graphs often exhibit asymptotic behavior, meaning that the graph approaches a horizontal asymptote as the input value increases. This asymptote represents the minimum value that the quantity can reach, and it is a key feature of exponential decay graphs.
Feature 4: Rapid Initial Decrease Exponential decay graphs typically exhibit a rapid initial decrease, followed by a slower decrease as the input value increases. This rapid initial decrease is a characteristic feature of exponential decay, and it is often used to identify exponential decay in graphs.

Feature 5: Exponential Function The final feature of an exponential decay graph is the presence of an exponential function. Exponential decay graphs can be modeled using exponential functions of the form y = ab^x, where a and b are constants. This exponential function is a key characteristic of exponential decay graphs, and it is often used to identify exponential decay in graphs.

By identifying these 5 key graph features, you can determine whether a graph represents exponential decay. Remember to look for a decreasing trend, non-linear relationship, asymptotic behavior, rapid initial decrease, and the presence of an exponential function.
Real-World Applications Exponential decay has numerous real-world applications, including:
- Population growth and decay
- Chemical reactions and half-lives
- Nuclear decay and radioactive materials
- Financial modeling and compound interest
- Electrical engineering and circuit analysis
In each of these applications, exponential decay plays a crucial role in understanding and modeling the behavior of complex systems.
Conclusion In conclusion, exponential decay is a fundamental concept in mathematics that can be identified by specific graph features. By recognizing these features, you can determine whether a graph represents exponential decay and apply this knowledge to real-world problems. Whether you are a student, scientist, or engineer, understanding exponential decay is essential for modeling and analyzing complex systems.
Gallery of Exponential Decay Graphs





FAQ
What is exponential decay?
+Exponential decay is a process where a quantity decreases exponentially over time.
How can I identify exponential decay in a graph?
+Look for a decreasing trend, non-linear relationship, asymptotic behavior, rapid initial decrease, and the presence of an exponential function.
What are some real-world applications of exponential decay?
+Exponential decay has numerous real-world applications, including population growth and decay, chemical reactions and half-lives, nuclear decay and radioactive materials, financial modeling and compound interest, and electrical engineering and circuit analysis.