What Is 40 To The Power Of 2

Quick Links :

Let's dive into the world of exponents!

When we say "40 to the power of 2," we're referring to the mathematical operation of raising 40 to the second power, denoted as 40². This means multiplying 40 by itself.

40² = 40 × 40 = 1600

So, 40 to the power of 2 is equal to 1600!

Understanding Exponents

Exponents are shorthand notation for repeated multiplication. The exponent (in this case, 2) indicates how many times the base number (40) should be multiplied by itself.

Here are a few more examples to illustrate this:

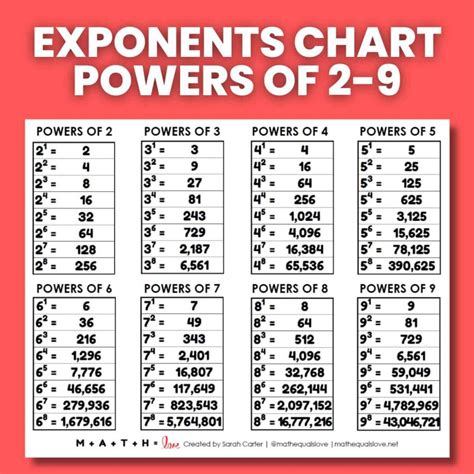
• 2³ = 2 × 2 × 2 = 8 (2 to the power of 3)
• 3⁴ = 3 × 3 × 3 × 3 = 81 (3 to the power of 4)
• 5² = 5 × 5 = 25 (5 to the power of 2)

Applications of Exponents

Exponents have numerous applications in mathematics, science, and engineering. They're used to model population growth, calculate compound interest, and describe the behavior of physical systems.

For instance, the formula for compound interest is A = P(1 + r)ⁿ, where A is the future value, P is the principal amount, r is the interest rate, and n is the number of times the interest is compounded.

Real-World Examples

Exponents are all around us, and here are a few examples:

• Population growth: The population of a city can be modeled using the formula P(t) = P0 * (1 + r)ⁿ, where P0 is the initial population, r is the growth rate, and t is time.
• Computer science: Exponents are used in algorithms for solving complex problems, such as finding the shortest path in a graph.
• Physics: The formula for the area of a circle is A = πr², where A is the area, π is a constant, and r is the radius.

Calculating Exponents

There are several ways to calculate exponents, depending on the size of the numbers involved. Here are a few methods:

• Long multiplication: This involves multiplying the base number by itself repeatedly.
• Exponentiation by squaring: This method involves breaking down the exponent into smaller parts and using the fact that (a²)² = a⁴.
• Using a calculator: Most calculators have an exponentiation function that can be used to calculate exponents quickly.

Conclusion

In this article, we explored the concept of exponents, specifically 40 to the power of 2. We discussed the definition, applications, and real-world examples of exponents. We also touched on different methods for calculating exponents.

I hope you found this article informative and helpful. If you have any questions or topics you'd like to discuss, please leave a comment below!

FAQ Section: