Trigonometry is a fundamental branch of mathematics that deals with the relationships between the sides and angles of triangles. It has numerous applications in various fields, including physics, engineering, navigation, and computer science. One of the essential concepts in trigonometry is the sine, cosine, and tangent functions. In this article, we will delve into the concept of 3 cos(x) in trigonometry, exploring its meaning, significance, and applications.
What is 3 cos(x)?
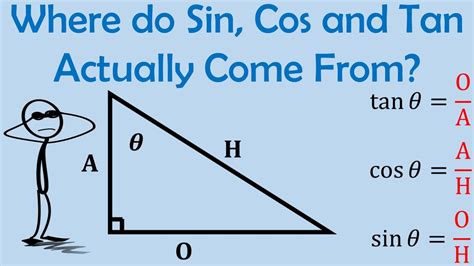
In trigonometry, cos(x) represents the cosine function, which is defined as the ratio of the length of the adjacent side to the length of the hypotenuse in a right-angled triangle. The cosine function is a fundamental trigonometric function that is used to describe the relationship between the angle and the ratio of the adjacent side to the hypotenuse.
3 cos(x) is an expression that represents three times the cosine of an angle x. In other words, it is the product of 3 and the cosine of the angle x. This expression is commonly used in trigonometric equations, identities, and formulas to describe various relationships between angles and side lengths in triangles.
Significance of 3 cos(x)
The expression 3 cos(x) has significant importance in trigonometry and its applications. Here are a few reasons why:
- Trigonometric identities: 3 cos(x) is used in various trigonometric identities, such as the triple angle formula, which states that cos(3x) = 4cos^3(x) - 3cos(x). This identity is useful in solving trigonometric equations and simplifying complex expressions.
- Graphical representation: The graph of 3 cos(x) is a sinusoidal curve that has an amplitude of 3 and a period of 2π. This graph is useful in visualizing the behavior of the cosine function and its applications in physics and engineering.
- Applications in physics and engineering: 3 cos(x) is used in various applications, such as simple harmonic motion, wave propagation, and electrical engineering. For example, in simple harmonic motion, the displacement of an object can be described by the equation x(t) = 3 cos(ωt + φ), where x(t) is the displacement at time t, ω is the angular frequency, and φ is the phase angle.
Working Mechanisms of 3 cos(x)
To understand the working mechanisms of 3 cos(x), let's consider a few examples:
- Simplifying trigonometric expressions: 3 cos(x) can be used to simplify complex trigonometric expressions, such as 3 cos(x) sin(x) = 3/2 sin(2x).
- Solving trigonometric equations: 3 cos(x) can be used to solve trigonometric equations, such as 3 cos(x) = 2 sin(x), which can be solved using the identity cos(x) = sin(π/2 - x).
- Graphical analysis: The graph of 3 cos(x) can be used to analyze the behavior of the cosine function and its applications in physics and engineering.
Practical Examples of 3 cos(x)
Here are a few practical examples of 3 cos(x) in trigonometry:
- Simple harmonic motion: The displacement of an object in simple harmonic motion can be described by the equation x(t) = 3 cos(ωt + φ), where x(t) is the displacement at time t, ω is the angular frequency, and φ is the phase angle.
- Wave propagation: The amplitude of a wave can be described by the equation A(x) = 3 cos(kx + φ), where A(x) is the amplitude at position x, k is the wave number, and φ is the phase angle.
- Electrical engineering: The voltage across a capacitor in an electrical circuit can be described by the equation V(t) = 3 cos(ωt + φ), where V(t) is the voltage at time t, ω is the angular frequency, and φ is the phase angle.
Gallery of Trigonometric Functions





Frequently Asked Questions
What is the significance of 3 cos(x) in trigonometry?
+3 cos(x) is significant in trigonometry as it is used in various trigonometric identities, graphical representation, and applications in physics and engineering.
How is 3 cos(x) used in simple harmonic motion?
+3 cos(x) is used in simple harmonic motion to describe the displacement of an object, where x(t) = 3 cos(ωt + φ), x(t) is the displacement at time t, ω is the angular frequency, and φ is the phase angle.
What is the graph of 3 cos(x) used for?
+The graph of 3 cos(x) is used to visualize the behavior of the cosine function and its applications in physics and engineering.
In conclusion, 3 cos(x) is a fundamental expression in trigonometry that has significant importance in various applications, including simple harmonic motion, wave propagation, and electrical engineering. Understanding the concept of 3 cos(x) is essential for solving trigonometric equations, simplifying complex expressions, and analyzing the behavior of the cosine function. We hope this article has provided a comprehensive explanation of 3 cos(x) and its applications in trigonometry.