What Comes After Four Fifths In Math

Quick Links :

In mathematics, when you're working with fractions, you often need to consider the next fraction in a sequence. When you ask what comes after four fifths, we're essentially looking for the next fraction in a sequence of increasing values.

Four fifths is represented mathematically as 4/5. To find the next fraction after 4/5, we need to increment the numerator (the top number) by 1 while keeping the denominator (the bottom number) the same. This results in the fraction 5/5.

So, what comes after four fifths is five fifths, which simplifies to 1 whole unit.

Here's a visualization to help illustrate this concept:

• 3/5 (three fifths)
• 4/5 (four fifths)
• 5/5 (five fifths, or 1 whole unit)

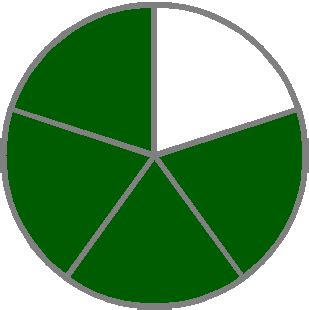
Think of it like a pie cut into five equal slices. If you have four slices (4/5), the next step is to have the entire pie, which is five slices (5/5) or 1 whole unit.

In summary, the fraction that comes after four fifths is five fifths, which is equivalent to 1 whole unit.

Understanding Fractions

Fractions are a fundamental concept in mathematics, representing a part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number), separated by a line called a vinculum.

• The numerator tells you how many equal parts you have.
• The denominator tells you how many parts the whole is divided into.

For example, in the fraction 3/4, the numerator 3 indicates that you have three equal parts, and the denominator 4 indicates that the whole is divided into four parts.

Fraction Basics

Here are some essential concepts related to fractions:

• Equivalent fractions: Fractions that have the same value, but different numerators and denominators. For example, 1/2 is equivalent to 2/4, 3/6, and so on.
• Simplifying fractions: Reducing a fraction to its simplest form by dividing both the numerator and denominator by the greatest common divisor (GCD). For example, 4/8 can be simplified to 1/2.
• Adding and subtracting fractions: Combining fractions with the same denominator by adding or subtracting the numerators. For example, 1/4 + 1/4 = 2/4, and 2/4 - 1/4 = 1/4.
• Multiplying fractions: Multiplying the numerators and denominators separately. For example, (1/2) × (3/4) = 3/8.
• Dividing fractions: Inverting the second fraction (i.e., flipping the numerator and denominator) and then multiplying. For example, (1/2) ÷ (3/4) = (1/2) × (4/3) = 4/6.

Real-World Applications of Fractions

Fractions are used in various real-world contexts, including:

• Cooking: Measuring ingredients, scaling recipes, and adjusting cooking times.
• Music: Representing rhythm, time signatures, and musical intervals.
• Finance: Calculating interest rates, investment returns, and financial ratios.
• Science: Expressing quantities, proportions, and rates of change.
• Architecture: Designing buildings, calculating dimensions, and scaling plans.

In conclusion, understanding fractions is essential for mathematical literacy and has numerous practical applications. By grasping the basics of fractions, you'll be better equipped to tackle a wide range of problems and challenges in various fields.

Practice Problems

Try solving these fraction problems to reinforce your understanding:

• Simplify the fraction 6/8.
• Add 1/4 and 1/6.
• Multiply 2/3 and 3/4.
• Divide 3/4 by 2/3.

Answers:

• 6/8 simplifies to 3/4.
• 1/4 + 1/6 = 5/12.
• (2/3) × (3/4) = 6/12 = 1/2.
• (3/4) ÷ (2/3) = (3/4) × (3/2) = 9/8.

Remember, practice makes perfect! The more you work with fractions, the more comfortable you'll become with these essential mathematical concepts.

Gallery of Printable Fraction Resources