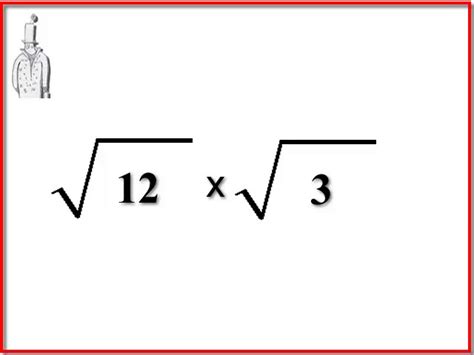Simplifying The Square Root Of -12 Explained

Quick Links :

The concept of square roots has been a fundamental part of mathematics for centuries, allowing us to find the value of a number that, when multiplied by itself, gives a specified value. However, when dealing with negative numbers, the concept of square roots becomes more complex. In this article, we will delve into the world of imaginary numbers and explore the simplification of the square root of -12.

Understanding Square Roots

Before we dive into the simplification of the square root of -12, it's essential to understand the concept of square roots. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

However, when dealing with negative numbers, the concept of square roots becomes more complex. The square of any real number is always positive, or zero. This means that there is no real number that can be squared to give a negative value. To overcome this limitation, mathematicians introduced the concept of imaginary numbers.

What are Imaginary Numbers?

Imaginary numbers are a mathematical concept that allows us to extend the real number system to include numbers that can be squared to give negative values. Imaginary numbers are denoted by the symbol "i" and are defined as the square root of -1.

The concept of imaginary numbers may seem abstract, but it has numerous applications in mathematics, physics, and engineering. Imaginary numbers allow us to solve equations that cannot be solved using only real numbers.

Simplifying the Square Root of -12

Now that we have a basic understanding of imaginary numbers, let's simplify the square root of -12.

The square root of -12 can be written as √(-12). To simplify this expression, we can rewrite -12 as -1 × 12.

Using the properties of square roots, we can rewrite the expression as:

√(-12) = √(-1) × √12

Since √(-1) is equal to "i", we can rewrite the expression as:

√(-12) = i√12

Now, we can simplify the square root of 12. The square root of 12 can be written as √(4 × 3), which is equal to √4 × √3.

Using the property of square roots, we can rewrite the expression as:

√(-12) = i√4 × √3

Since √4 is equal to 2, we can rewrite the expression as:

√(-12) = i2√3

Finally, we can simplify the expression by rewriting it as:

√(-12) = 2i√3

In conclusion, the simplified square root of -12 is 2i√3.

Gallery of Simplifying the Square Root of -12

Frequently Asked Questions

What is the square root of -12?

The square root of -12 can be written as √(-12), which is equal to 2i√3.

What are imaginary numbers?

Imaginary numbers are a mathematical concept that allows us to extend the real number system to include numbers that can be squared to give negative values.

How do you simplify the square root of -12?

To simplify the square root of -12, you can rewrite -12 as -1 × 12 and then use the properties of square roots to simplify the expression.

What is the importance of imaginary numbers in mathematics?

Imaginary numbers have numerous applications in mathematics, physics, and engineering, allowing us to solve equations that cannot be solved using only real numbers.

Conclusion

In this article, we explored the concept of imaginary numbers and simplified the square root of -12. We discovered that the simplified square root of -12 is 2i√3. Imaginary numbers are a fundamental concept in mathematics, allowing us to extend the real number system and solve complex equations.

We hope that this article has provided you with a deeper understanding of imaginary numbers and the simplification of the square root of -12. If you have any questions or need further clarification, please don't hesitate to ask.