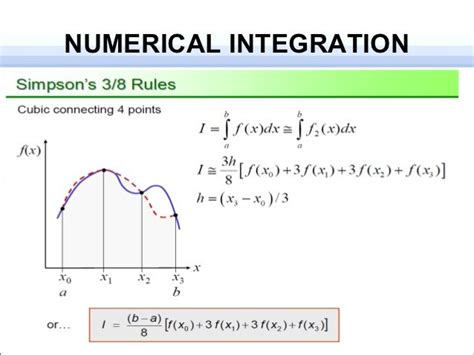
The world of numerical integration has undergone significant transformations over the years, with various methods and techniques being developed to tackle complex problems. One such innovation that has garnered considerable attention is the Sobol sequence, a groundbreaking application that has revolutionized the field of numerical integration.
What is the Sobol Sequence?

The Sobol sequence is a quasi-random sequence that was first introduced by the mathematician Ilya Sobol in the 1960s. It is a type of low-discrepancy sequence that is designed to distribute points uniformly within a multi-dimensional space. The sequence is generated using a set of polynomials and has been widely used in various fields, including numerical integration, Monte Carlo simulations, and optimization problems.
How Does the Sobol Sequence Work?
The Sobol sequence works by generating a set of points that are uniformly distributed within a multi-dimensional space. The sequence is generated using a set of polynomials that are designed to produce a set of points that are as uniform as possible. The points are generated in a way that minimizes the discrepancy between the points and the uniform distribution.Benefits of the Sobol Sequence
The Sobol sequence has several benefits that make it an attractive choice for numerical integration. Some of the benefits include:- Improved accuracy: The Sobol sequence is designed to produce a set of points that are as uniform as possible, which leads to improved accuracy in numerical integration.
- Increased efficiency: The Sobol sequence can be generated quickly and efficiently, making it an attractive choice for large-scale numerical integration problems.
- Reduced variance: The Sobol sequence has a lower variance than traditional random sequences, which leads to more accurate results.
Applications of the Sobol Sequence
The Sobol sequence has a wide range of applications in various fields, including:- Numerical integration: The Sobol sequence is widely used in numerical integration problems, such as evaluating multi-dimensional integrals and computing expectations.
- Monte Carlo simulations: The Sobol sequence is used in Monte Carlo simulations to generate random samples and estimate expectations.
- Optimization problems: The Sobol sequence is used in optimization problems to generate a set of points that are uniformly distributed within the feasible region.
Comparison with Other Methods
The Sobol sequence is often compared with other methods, such as the Monte Carlo method and the quasi-Monte Carlo method. While these methods have their own strengths and weaknesses, the Sobol sequence has several advantages that make it an attractive choice for numerical integration problems.Conclusion
In conclusion, the Sobol sequence is a powerful tool for numerical integration that offers several benefits, including improved accuracy, increased efficiency, and reduced variance. Its applications are diverse, ranging from numerical integration to optimization problems. As the field of numerical integration continues to evolve, the Sobol sequence is likely to remain a game-changer in the industry.





What is the Sobol sequence?
+The Sobol sequence is a quasi-random sequence that is designed to distribute points uniformly within a multi-dimensional space.
What are the benefits of the Sobol sequence?
+The Sobol sequence has several benefits, including improved accuracy, increased efficiency, and reduced variance.
What are the applications of the Sobol sequence?
+The Sobol sequence has a wide range of applications, including numerical integration, Monte Carlo simulations, and optimization problems.
We hope this article has provided you with a comprehensive understanding of the Sobol sequence and its applications. If you have any further questions or would like to know more about the topic, please feel free to comment below.