5 Ways To Master The Distance Formula

Quick Links :

In mathematics, the distance formula is a fundamental concept used to calculate the distance between two points in a coordinate plane. Mastering the distance formula is essential for students, professionals, and anyone who works with coordinates and geometry. In this article, we will explore five ways to master the distance formula, making it easier to apply in various mathematical and real-world problems.

The distance formula is a straightforward concept, but it can be daunting for some individuals. With practice and the right approach, anyone can become proficient in using the distance formula. Whether you're a student looking to improve your math skills or a professional seeking to enhance your analytical abilities, this article will provide you with the tools and techniques necessary to master the distance formula.

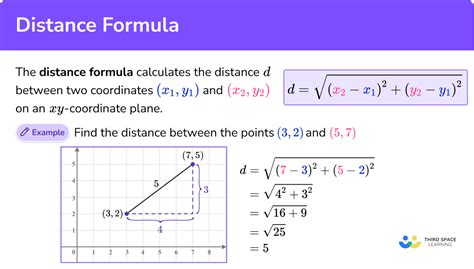
One of the primary reasons individuals struggle with the distance formula is the lack of understanding of its components. The distance formula is derived from the Pythagorean theorem, which states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides. The distance formula is a direct application of this theorem, where the distance between two points (x1, y1) and (x2, y2) is calculated as:

√((x2 - x1)^2 + (y2 - y1)^2)

Understanding the Components of the Distance Formula

Before diving into the five ways to master the distance formula, it's essential to understand its components. The distance formula consists of four main parts:

• (x2 - x1) represents the horizontal distance between the two points
• (y2 - y1) represents the vertical distance between the two points
• The exponent 2 indicates that the differences are squared
• The square root symbol (√) indicates that the result is the square root of the sum of the squared differences

Way 1: Practice with Simple Coordinates

One of the most effective ways to master the distance formula is to practice with simple coordinates. Start by using points with integer coordinates, such as (0, 0) and (3, 4). Calculate the distance between these points using the distance formula and verify your answer by plotting the points on a coordinate plane.

For example, let's calculate the distance between points (2, 3) and (4, 6):

√((4 - 2)^2 + (6 - 3)^2) = √(2^2 + 3^2) = √(4 + 9) = √13

Way 2: Use Real-World Applications

Another way to master the distance formula is to use real-world applications. The distance formula is used in various fields, such as physics, engineering, and geography. By applying the distance formula to real-world problems, you'll gain a deeper understanding of its significance and relevance.

For example, let's say you're a pilot flying from point A to point B. If you know the coordinates of both points, you can use the distance formula to calculate the distance between them. This information can help you determine the fuel consumption, flight time, and other essential factors.

Way 3: Visualize the Coordinate Plane

Visualizing the coordinate plane is an excellent way to master the distance formula. By plotting points on a coordinate plane, you can see the relationship between the points and the distance between them. This visualization will help you understand how the distance formula works and make it easier to apply.

For example, let's plot points (0, 0), (3, 4), and (6, 8) on a coordinate plane. By drawing a line between each pair of points, you can see the distance between them and how it relates to the distance formula.

Way 4: Use Online Resources and Tools

There are many online resources and tools available to help you master the distance formula. Websites like Khan Academy, Mathway, and GeoGebra offer interactive lessons, practice exercises, and calculators to help you understand and apply the distance formula.

For example, you can use an online distance formula calculator to verify your answers and check your work. These calculators can also help you visualize the coordinate plane and plot points.

Way 5: Create Your Own Problems

Creating your own problems is an excellent way to master the distance formula. By generating your own problems, you'll be able to practice applying the distance formula to different scenarios and coordinates. This will help you develop your critical thinking skills and problem-solving abilities.

For example, let's create a problem where we need to calculate the distance between two points on a map. We can use a map or a coordinate plane to generate the coordinates of the two points and then apply the distance formula to calculate the distance between them.

In conclusion, mastering the distance formula requires practice, patience, and persistence. By following these five ways to master the distance formula, you'll be able to apply it confidently and accurately in various mathematical and real-world problems. Remember to practice with simple coordinates, use real-world applications, visualize the coordinate plane, use online resources and tools, and create your own problems. With time and effort, you'll become proficient in using the distance formula and unlock its full potential.

Gallery of Distance Formula Examples