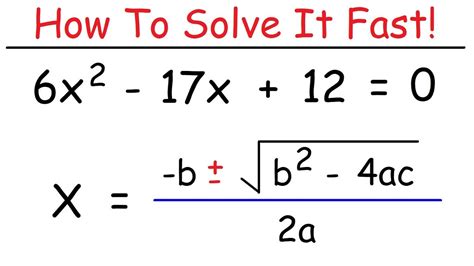The world of mathematics is full of complexities and nuances, and quadratic applications are no exception. These equations, which involve squared variables, are a fundamental part of algebra and are used to model a wide range of real-world phenomena. From physics and engineering to economics and finance, quadratic applications are an essential tool for anyone looking to understand and analyze complex systems.

However, mastering quadratic applications can be a daunting task, especially for those who are new to algebra. The good news is that with practice and persistence, anyone can become proficient in quadratic applications. Here are five ways to help you master quadratic applications:
1. Understand the Basics
Before you can start mastering quadratic applications, you need to understand the basics of quadratic equations. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two. The general form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are constants, and x is the variable.

To solve quadratic equations, you can use a variety of methods, including factoring, completing the square, and using the quadratic formula. The quadratic formula is:
x = (-b ± √(b^2 - 4ac)) / 2a
This formula will give you the solutions to the quadratic equation.
2. Practice, Practice, Practice
Practice is key to mastering quadratic applications. The more you practice, the more comfortable you will become with solving quadratic equations and applying them to real-world problems. Here are a few tips to help you practice:
- Start with simple quadratic equations and gradually move on to more complex ones.
- Use online resources, such as Khan Academy or MIT OpenCourseWare, to find practice problems and video lectures.
- Practice solving quadratic equations by hand, as well as using calculators or computer software.

3. Use Real-World Examples
One of the best ways to master quadratic applications is to use real-world examples. Quadratic equations are used to model a wide range of phenomena, from the trajectory of a projectile to the growth of a population. By using real-world examples, you can see the relevance of quadratic equations and make them more meaningful.
Here are a few examples of how quadratic equations are used in real-world applications:
- Physics: Quadratic equations are used to model the motion of objects, including the trajectory of projectiles and the motion of pendulums.
- Engineering: Quadratic equations are used to design and optimize systems, including bridges and electronic circuits.
- Economics: Quadratic equations are used to model the behavior of economic systems, including the supply and demand of goods.

4. Use Technology
Technology can be a powerful tool for mastering quadratic applications. There are a wide range of software programs and apps that can help you solve quadratic equations and visualize the results. Here are a few examples:
- Graphing calculators: Graphing calculators can be used to visualize the solutions to quadratic equations and explore the properties of quadratic functions.
- Computer algebra systems: Computer algebra systems, such as Mathematica or Maple, can be used to solve quadratic equations and manipulate algebraic expressions.
- Online tools: There are a wide range of online tools, including quadratic equation solvers and graphing utilities, that can be used to help you master quadratic applications.

5. Seek Help When Needed
Finally, don't be afraid to seek help when you need it. Mastering quadratic applications can be challenging, and it's okay to ask for help along the way. Here are a few resources you can use to get help:
- Teachers and tutors: If you're taking a class or working with a tutor, don't hesitate to ask for help when you need it.
- Online forums: There are a wide range of online forums, including Reddit and Stack Exchange, where you can ask for help and get feedback from other students and experts.
- Study groups: Joining a study group can be a great way to get help and support from other students who are also working to master quadratic applications.

Gallery of Quadratic Applications:






FAQs:
What is a quadratic equation?
+A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two.
How do I solve a quadratic equation?
+There are several methods to solve a quadratic equation, including factoring, completing the square, and using the quadratic formula.
What are some real-world applications of quadratic equations?
+Quadratic equations are used to model a wide range of real-world phenomena, including the motion of objects, the growth of populations, and the behavior of economic systems.