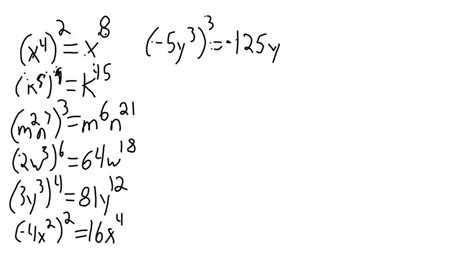Mathematics has been an integral part of various fields, including physics, engineering, and architecture. One fundamental concept that has numerous applications in these fields is monomials. Monomials, in essence, are algebraic expressions consisting of a single term, which can be a number, a variable, or a combination of both. The simplicity of monomials often leads to their underestimation, but they play a crucial role in simplifying complex geometric applications. In this article, we will explore five ways in which monomials contribute to the simplification of geometric problems.
What are Monomials?
Before diving into the applications of monomials in geometry, it is essential to understand the basics of monomials. Monomials are algebraic expressions that consist of only one term. This term can be a number, a variable, or a combination of both. For example, 3x, 2y, and 5 are all monomials. Monomials can be combined using addition, subtraction, multiplication, and division to form more complex expressions.

Applications of Monomials in Geometry
Monomials have numerous applications in geometry, from calculating the area of triangles to determining the volume of 3D shapes. Here are five ways monomials simplify geometric applications:
1. Calculating Perimeter and Area
One of the most straightforward applications of monomials in geometry is calculating the perimeter and area of triangles and rectangles. For instance, the area of a rectangle can be calculated using the formula: Area = Length × Width. In this formula, the length and width are represented by monomials. By substituting the values of the length and width, we can calculate the area of the rectangle.

2. Determining Volumes of 3D Shapes
Monomials are also used to determine the volumes of 3D shapes, such as cuboids and cones. The volume of a cuboid, for example, can be calculated using the formula: Volume = Length × Width × Height. In this formula, the length, width, and height are represented by monomials. By substituting the values of these monomials, we can calculate the volume of the cuboid.

3. Finding Surface Areas
Monomials are also used to find the surface areas of 3D shapes. The surface area of a sphere, for instance, can be calculated using the formula: Surface Area = 4 × π × Radius^2. In this formula, the radius is represented by a monomial. By substituting the value of the radius, we can calculate the surface area of the sphere.

4. Analyzing Geometric Transformations
Monomials can also be used to analyze geometric transformations, such as rotations and reflections. For example, a rotation of a point (x, y) about the origin can be represented by the monomial: (x cos θ - y sin θ, x sin θ + y cos θ). By analyzing this monomial, we can determine the new coordinates of the point after the rotation.

5. Solving Trigonometric Problems
Finally, monomials can be used to solve trigonometric problems, such as finding the lengths of sides in a right-angled triangle. The Pythagorean theorem, for example, states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This theorem can be represented by the monomial: a^2 + b^2 = c^2. By analyzing this monomial, we can determine the length of the hypotenuse.







Gallery of Monomial Applications in Geometry
Monomials are an essential part of algebra, and their applications in geometry are diverse and numerous. From calculating the perimeter and area of triangles to determining the volumes of 3D shapes, monomials play a crucial role in simplifying complex geometric problems. By understanding the basics of monomials and their applications, we can develop a deeper appreciation for the beauty and complexity of geometry.
What is a monomial?
+A monomial is an algebraic expression consisting of a single term, which can be a number, a variable, or a combination of both.
How are monomials used in geometry?
+Monomials are used to calculate the perimeter and area of triangles and rectangles, determine the volumes of 3D shapes, analyze geometric transformations, and solve trigonometric problems.
What is the Pythagorean theorem?
+The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides in a right-angled triangle.
We hope you found this article informative and engaging. If you have any questions or would like to share your thoughts on the applications of monomials in geometry, please leave a comment below.