Find Gcf Of 28, 14, 36 In 3 Easy Steps

Quick Links :

Finding the greatest common factor (GCF) of three numbers can be a straightforward process. Here's how to find the GCF of 28, 14, and 36 in 3 easy steps.

Step 1: List the Factors of Each Number

To find the GCF, we need to list the factors of each number. A factor is a number that divides another number exactly without leaving a remainder.

• Factors of 28: 1, 2, 4, 7, 14, 28
• Factors of 14: 1, 2, 7, 14
• Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

Step 2: Identify the Common Factors

Next, we need to identify the common factors among the three numbers.

• Common factors of 28, 14, and 36: 1, 2

Notice that 1 and 2 are the only factors that appear in all three lists.

Step 3: Find the Greatest Common Factor

The GCF is the largest common factor among the numbers. In this case, the greatest common factor of 28, 14, and 36 is 2.

Therefore, the GCF of 28, 14, and 36 is 2.

I hope this helps! Do you have any other questions about finding the GCF?

More Tips on Finding the GCF

Finding the GCF can be a useful skill in math and real-life applications. Here are some additional tips to help you find the GCF:

• Use a Venn diagram to visualize the common factors among the numbers.
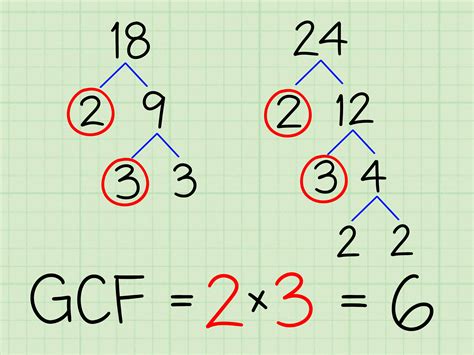
• Use a factor tree to break down each number into its prime factors.
• Look for patterns and relationships among the numbers.

Example of Finding the GCF Using a Factor Tree

Let's use a factor tree to find the GCF of 28, 14, and 36.

• Factor tree of 28: 28 = 2 × 2 × 7
• Factor tree of 14: 14 = 2 × 7
• Factor tree of 36: 36 = 2 × 2 × 3 × 3

Notice that the factor tree of each number shows the prime factors. The common prime factors among the numbers are 2 and 7. Therefore, the GCF of 28, 14, and 36 is 2.

Finding the GCF of More Than Three Numbers

Finding the GCF of more than three numbers can be a bit more challenging, but the process is similar.

• List the factors of each number.
• Identify the common factors among the numbers.
• Find the greatest common factor.

For example, let's find the GCF of 28, 14, 36, and 42.

• Factors of 28: 1, 2, 4, 7, 14, 28

• Factors of 14: 1, 2, 7, 14

• Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

• Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42

• Common factors of 28, 14, 36, and 42: 1, 2, 7

• Greatest common factor: 2

Therefore, the GCF of 28, 14, 36, and 42 is 2.

I hope this helps! Do you have any other questions about finding the GCF?

Why is Finding the GCF Important?

Finding the GCF is an important skill in math and real-life applications. Here are some reasons why finding the GCF is important:

• Simplifying fractions: Finding the GCF can help simplify fractions by reducing them to their lowest terms.
• Reducing complexity: Finding the GCF can help reduce complex math problems by breaking them down into simpler components.
• Identifying patterns: Finding the GCF can help identify patterns and relationships among numbers.

For example, let's simplify the fraction 28/42 by finding the GCF.

• GCF of 28 and 42: 2, 7, 14
• Simplified fraction: 2/3

Therefore, the simplified fraction is 2/3.

I hope this helps! Do you have any other questions about finding the GCF?

Gallery of Printable GCF Examples