Discrete mathematics is a branch of mathematics that deals with mathematical structures that are fundamentally discrete, meaning they are made up of individual, distinct elements rather than continuous values. While it may seem abstract, discrete mathematics has a wide range of practical applications in the real world. Here are 10 ways discrete mathematics solves real-world problems:
1. Computer Networking

Discrete mathematics is crucial in the design and analysis of computer networks. Graph theory, a branch of discrete mathematics, is used to model and optimize network topologies, ensuring efficient data transmission and minimizing delays.
Key Concepts:
- Graph theory
- Network topology
- Optimization algorithms
2. Cryptography

Discrete mathematics provides the mathematical foundations for cryptography, enabling secure data transmission over the internet. Number theory, in particular, is used to develop cryptographic protocols, such as RSA and elliptic curve cryptography.
Key Concepts:
- Number theory
- Cryptographic protocols
- Secure data transmission
3. Coding Theory

Discrete mathematics is used to develop error-correcting codes, which are essential in digital communication systems. Coding theory, a branch of discrete mathematics, provides the mathematical tools to design and analyze error-correcting codes.
Key Concepts:
- Coding theory
- Error-correcting codes
- Digital communication systems
4. Data Analysis
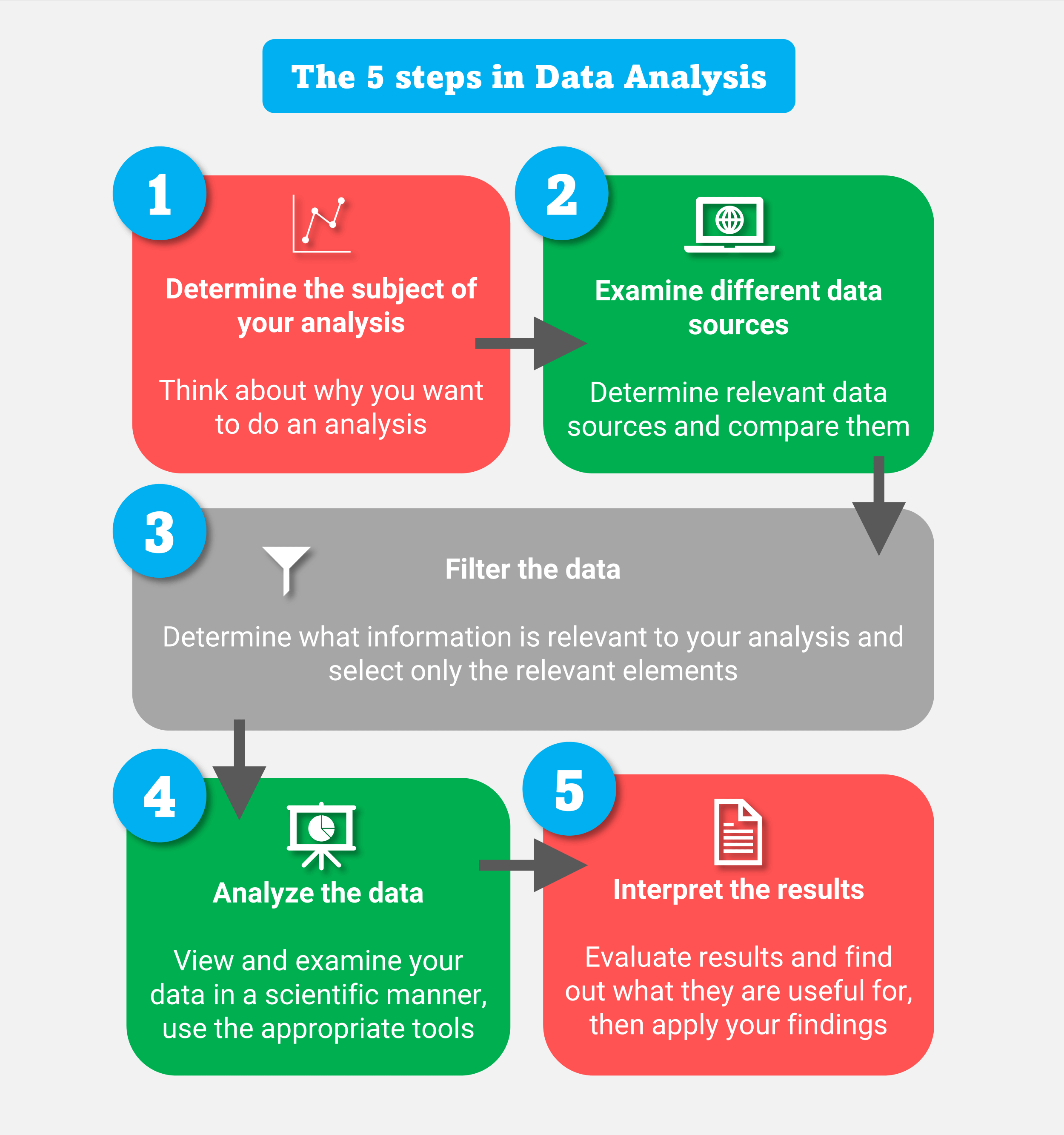
Discrete mathematics provides the mathematical foundations for data analysis, enabling the extraction of insights from large datasets. Combinatorics, a branch of discrete mathematics, is used to develop algorithms for data analysis.
Key Concepts:
- Combinatorics
- Data analysis
- Algorithm development
5. Optimization

Discrete mathematics provides the mathematical tools to solve optimization problems, which are ubiquitous in real-world applications. Optimization algorithms, developed using discrete mathematics, are used to find the best solution among a set of possible solutions.
Key Concepts:
- Optimization algorithms
- Linear programming
- Integer programming
6. Computational Biology

Discrete mathematics is used in computational biology to analyze and model biological systems. Graph theory, in particular, is used to model protein-protein interactions and gene regulatory networks.
Key Concepts:
- Graph theory
- Biological network analysis
- Systems biology
7. Logistics and Transportation

Discrete mathematics is used in logistics and transportation to optimize routes and schedules. Graph theory, in particular, is used to model transportation networks and develop efficient routing algorithms.
Key Concepts:
- Graph theory
- Routing algorithms
- Scheduling
8. Finance

Discrete mathematics is used in finance to model and analyze financial systems. Probability theory, a branch of discrete mathematics, is used to model risk and uncertainty in financial markets.
Key Concepts:
- Probability theory
- Risk analysis
- Financial modeling
9. Computer Vision

Discrete mathematics is used in computer vision to develop algorithms for image and video analysis. Combinatorics, a branch of discrete mathematics, is used to develop algorithms for object recognition and tracking.
Key Concepts:
- Combinatorics
- Image and video analysis
- Object recognition
10. Social Network Analysis

Discrete mathematics is used in social network analysis to model and analyze social networks. Graph theory, in particular, is used to model social networks and develop algorithms for community detection and influence maximization.
Key Concepts:
- Graph theory
- Social network analysis
- Community detection
As we have seen, discrete mathematics has a wide range of practical applications in the real world. From computer networking to social network analysis, discrete mathematics provides the mathematical foundations for solving complex problems in various fields.






We hope this article has provided you with a comprehensive understanding of the importance of discrete mathematics in solving real-world problems. Whether you're a student or a professional, discrete mathematics is an essential tool to have in your toolkit.
What is discrete mathematics?
+Discrete mathematics is a branch of mathematics that deals with mathematical structures that are fundamentally discrete, meaning they are made up of individual, distinct elements rather than continuous values.
What are some practical applications of discrete mathematics?
+Discrete mathematics has a wide range of practical applications in computer networking, cryptography, coding theory, data analysis, optimization, computational biology, logistics and transportation, finance, computer vision, and social network analysis.
Why is discrete mathematics important?
+Discrete mathematics is important because it provides the mathematical foundations for solving complex problems in various fields. It is an essential tool to have in your toolkit, whether you're a student or a professional.