Discrete mathematics is a branch of mathematics that deals with individual, distinct elements rather than continuous values. It has numerous applications in computer science, information technology, and other fields, making it a fundamental subject for students and professionals alike. In this article, we will explore 8 discrete mathematics solutions that you need to know, including their principles, applications, and examples.
Discrete mathematics is a broad field that encompasses various topics, including set theory, combinatorics, graph theory, number theory, and algebra. Each of these areas has its unique principles and applications, which are essential for problem-solving in computer science, data analysis, and other fields.
1. Set Theory: A Fundamental Concept in Discrete Mathematics
Set theory is a fundamental concept in discrete mathematics that deals with the study of sets, which are collections of unique objects. Sets are used to define various mathematical structures, such as relations, functions, and graphs. Set theory has numerous applications in computer science, including data structures, algorithms, and software engineering.

Key Principles of Set Theory
- A set is a collection of unique objects, known as elements or members.
- Sets can be finite or infinite.
- Sets can be represented using various notations, such as roster form, set-builder form, and interval notation.
2. Combinatorics: Counting and Arranging Objects
Combinatorics is a branch of discrete mathematics that deals with the study of counting and arranging objects in various ways. It has numerous applications in computer science, including algorithms, data structures, and software engineering.

Key Principles of Combinatorics
- Permutations: arrangements of objects in a specific order.
- Combinations: selections of objects without regard to order.
- Recurrence relations: equations that define a sequence of numbers recursively.
3. Graph Theory: Modeling Relationships between Objects
Graph theory is a branch of discrete mathematics that deals with the study of graphs, which are mathematical structures used to model relationships between objects. It has numerous applications in computer science, including network analysis, database systems, and software engineering.

Key Principles of Graph Theory
- Graphs consist of vertices (nodes) and edges (connections between nodes).
- Graphs can be directed or undirected.
- Graphs can be weighted or unweighted.
4. Number Theory: Properties of Integers and Other Whole Numbers
Number theory is a branch of discrete mathematics that deals with the study of properties of integers and other whole numbers. It has numerous applications in computer science, including cryptography, coding theory, and algorithm design.

Key Principles of Number Theory
- Divisibility: properties of integers that are divisible by other integers.
- Primality: properties of prime numbers, which are integers that are divisible only by 1 and themselves.
- Congruences: equations that involve modular arithmetic.
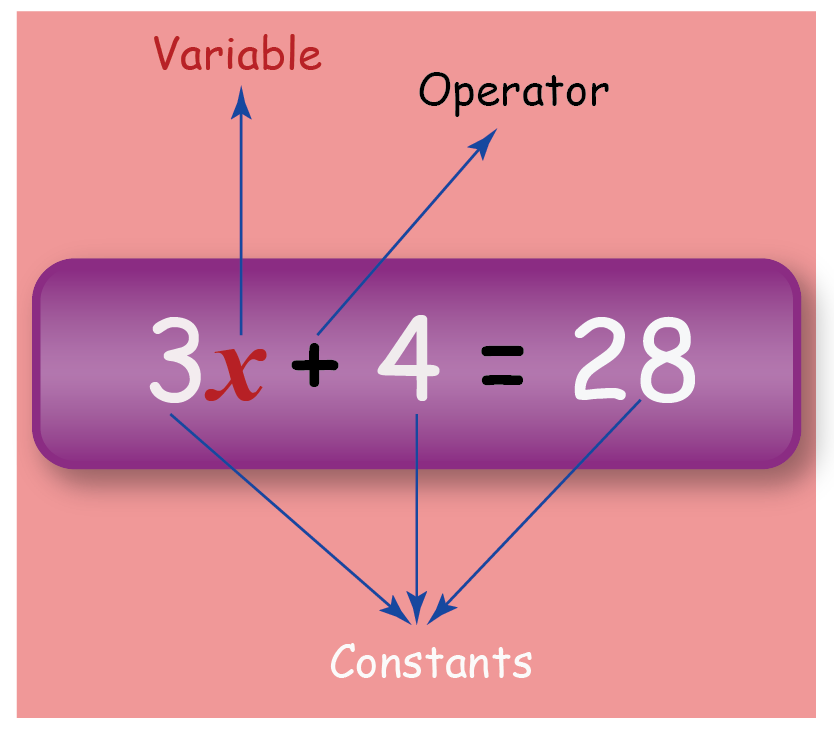
5. Algebra: Study of Variables and Their Relationships
Algebra is a branch of discrete mathematics that deals with the study of variables and their relationships. It has numerous applications in computer science, including algorithm design, computer graphics, and software engineering.

Key Principles of Algebra
- Variables: symbols that represent unknown values.
- Expressions: combinations of variables, constants, and operators.
- Equations: statements that assert the equality of two expressions.
6. Discrete Probability: Study of Random Events and Their Probabilities
Discrete probability is a branch of discrete mathematics that deals with the study of random events and their probabilities. It has numerous applications in computer science, including algorithm design, data analysis, and software engineering.

Key Principles of Discrete Probability
- Random events: events that occur randomly and unpredictably.
- Probabilities: numerical values that represent the likelihood of an event occurring.
- Probability distributions: functions that describe the probability of each possible outcome.
7. Discrete Optimization: Study of Optimal Solutions to Discrete Problems
Discrete optimization is a branch of discrete mathematics that deals with the study of optimal solutions to discrete problems. It has numerous applications in computer science, including algorithm design, data analysis, and software engineering.

Key Principles of Discrete Optimization
- Discrete problems: problems that involve discrete variables and constraints.
- Optimal solutions: solutions that maximize or minimize a objective function.
- Algorithms: procedures that solve discrete optimization problems.
8. Discrete Geometry: Study of Geometric Shapes and Their Properties
Discrete geometry is a branch of discrete mathematics that deals with the study of geometric shapes and their properties. It has numerous applications in computer science, including computer graphics, geographic information systems, and software engineering.

Key Principles of Discrete Geometry
- Geometric shapes: objects that have size, shape, and position.
- Properties: attributes of geometric shapes, such as area, perimeter, and volume.
- Transformations: operations that change the size, shape, or position of geometric shapes.
Gallery of Discrete Mathematics





FAQ
What is discrete mathematics?
+Discrete mathematics is a branch of mathematics that deals with individual, distinct elements rather than continuous values.
What are the applications of discrete mathematics?
+Discrete mathematics has numerous applications in computer science, information technology, and other fields, including algorithm design, data analysis, and software engineering.
What are the key principles of set theory?
+Set theory is based on several key principles, including the concept of a set, set notation, and set operations.
We hope this article has provided you with a comprehensive understanding of discrete mathematics and its applications. Whether you are a student, researcher, or professional, discrete mathematics is an essential subject that can help you solve complex problems and make informed decisions.
