Discrete mathematics is a branch of mathematics that deals with individual, distinct elements rather than continuous values. It is a fundamental subject that has numerous applications in various fields, including computer science, coding theory, cryptography, and more. In this article, we will explore five essential applications of discrete mathematics and how they impact our daily lives.
What is Discrete Mathematics?
Discrete mathematics is a study of mathematical structures that are fundamentally discrete, meaning they are made up of individual, distinct elements rather than continuous values. It involves the use of mathematical techniques, such as combinatorics, graph theory, and number theory, to analyze and solve problems. Discrete mathematics is essential in computer science, as it provides the mathematical foundations for computer programming, algorithms, and data structures.

Application 1: Computer Networking
Computer networking is a crucial application of discrete mathematics. Graph theory, a branch of discrete mathematics, is used to model and analyze computer networks. Network topology, routing algorithms, and network optimization are all based on graph theory. Discrete mathematics is used to design efficient algorithms for routing data packets, ensuring reliable communication, and optimizing network performance.
How Discrete Mathematics is Used in Computer Networking
Discrete mathematics is used in computer networking in several ways:
- Graph theory is used to model network topology and analyze network connectivity.
- Combinatorial algorithms are used to optimize network routing and ensure efficient data transfer.
- Number theory is used to develop secure encryption algorithms for data transmission.

Application 2: Coding Theory
Coding theory is another essential application of discrete mathematics. Error-correcting codes, such as Reed-Solomon codes and Hamming codes, are used to detect and correct errors in digital data transmission. Discrete mathematics is used to develop efficient algorithms for encoding and decoding data, ensuring reliable communication.
How Discrete Mathematics is Used in Coding Theory
Discrete mathematics is used in coding theory in several ways:
- Combinatorial algorithms are used to develop efficient encoding and decoding algorithms.
- Number theory is used to develop secure encryption algorithms for data transmission.
- Graph theory is used to analyze code structure and optimize code performance.

Application 3: Cryptography
Cryptography is a critical application of discrete mathematics. Discrete mathematics is used to develop secure encryption algorithms, such as RSA and elliptic curve cryptography, to protect data transmission. Number theory, combinatorics, and graph theory are all used to develop efficient and secure encryption algorithms.
How Discrete Mathematics is Used in Cryptography
Discrete mathematics is used in cryptography in several ways:
- Number theory is used to develop secure encryption algorithms, such as RSA and elliptic curve cryptography.
- Combinatorial algorithms are used to develop efficient decryption algorithms.
- Graph theory is used to analyze cryptographic protocols and optimize security.

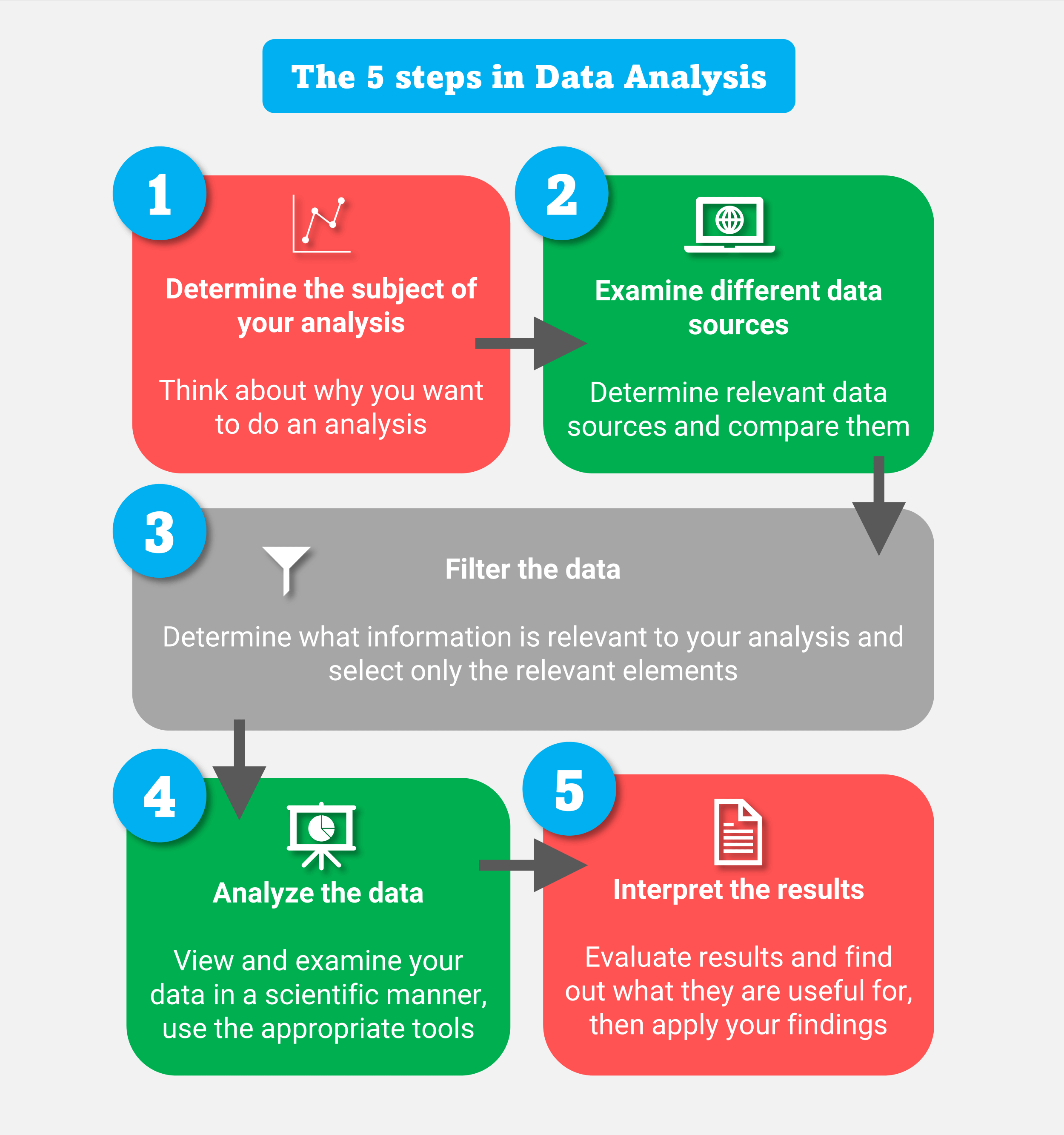
Application 4: Data Analysis
Data analysis is another essential application of discrete mathematics. Discrete mathematics is used to develop efficient algorithms for data analysis, such as clustering, classification, and regression. Combinatorial algorithms and graph theory are used to analyze large datasets and identify patterns.
How Discrete Mathematics is Used in Data Analysis
Discrete mathematics is used in data analysis in several ways:
- Combinatorial algorithms are used to develop efficient clustering and classification algorithms.
- Graph theory is used to analyze network data and identify patterns.
- Number theory is used to develop secure data encryption algorithms.
Application 5: Optimization
Optimization is a critical application of discrete mathematics. Discrete mathematics is used to develop efficient algorithms for optimization problems, such as scheduling, resource allocation, and logistics. Combinatorial algorithms and graph theory are used to optimize complex systems and processes.
How Discrete Mathematics is Used in Optimization
Discrete mathematics is used in optimization in several ways:
- Combinatorial algorithms are used to develop efficient scheduling and resource allocation algorithms.
- Graph theory is used to analyze network data and optimize logistics.
- Number theory is used to develop secure encryption algorithms for data transmission.







What is discrete mathematics?
+Discrete mathematics is a branch of mathematics that deals with individual, distinct elements rather than continuous values.
What are some applications of discrete mathematics?
+Discrete mathematics has numerous applications in computer science, coding theory, cryptography, data analysis, and optimization.
How is discrete mathematics used in computer networking?
+Discrete mathematics is used in computer networking to model network topology, analyze network connectivity, and optimize network performance.
In conclusion, discrete mathematics has numerous essential applications in various fields, including computer science, coding theory, cryptography, data analysis, and optimization. Its techniques, such as combinatorics, graph theory, and number theory, are used to develop efficient algorithms, analyze complex systems, and optimize processes. Understanding discrete mathematics is crucial for developing innovative solutions to real-world problems.
