Discrete mathematics, a branch of mathematics that deals with individual, distinct elements rather than continuous values, has a profound impact on various real-life applications. From computer science and coding theory to network analysis and cryptography, discrete math plays a crucial role in shaping the world we live in. In this article, we will explore five ways discrete math impacts real-life applications.
Computer Science and Coding Theory
Discrete mathematics is the foundation of computer science. It provides the mathematical framework for understanding and analyzing algorithms, data structures, and software design. Computer scientists use discrete math to develop efficient algorithms, ensure data integrity, and optimize system performance.
For instance, graph theory, a branch of discrete mathematics, is used to optimize network routing, scheduling, and resource allocation. Google's algorithm for ranking web pages, known as PageRank, relies heavily on graph theory. Similarly, coding theory, which is based on discrete math, is used to develop error-correcting codes that ensure data transmission accuracy.

Network Analysis and Optimization
Discrete math is used to analyze and optimize complex networks, such as social networks, transportation networks, and communication networks. Network analysis helps us understand the structure and behavior of these networks, identify patterns and anomalies, and optimize their performance.
For example, network analysis is used to optimize traffic flow in cities, predict the spread of diseases, and identify influential individuals in social networks. Discrete math also helps us design more efficient algorithms for network optimization, such as finding the shortest path between two nodes or identifying the minimum spanning tree of a network.
Cryptography and Cybersecurity
Discrete mathematics plays a critical role in cryptography and cybersecurity. Cryptographic algorithms, such as RSA and elliptic curve cryptography, rely on discrete math to ensure secure data transmission and authentication.
Discrete math is used to develop secure encryption algorithms, digital signatures, and cryptographic protocols. For instance, the Advanced Encryption Standard (AES) uses discrete math to ensure secure data encryption. Similarly, cryptographic protocols, such as SSL/TLS, rely on discrete math to establish secure connections over the internet.

Optimization and Logistics
Discrete mathematics is used to optimize complex systems, such as supply chains, logistics, and resource allocation. Discrete math helps us develop efficient algorithms for solving optimization problems, such as finding the shortest path, minimum spanning tree, or maximum flow in a network.
For example, Amazon uses discrete math to optimize its supply chain and logistics. Discrete math helps Amazon identify the most efficient routes for delivery, optimize inventory management, and reduce transportation costs.
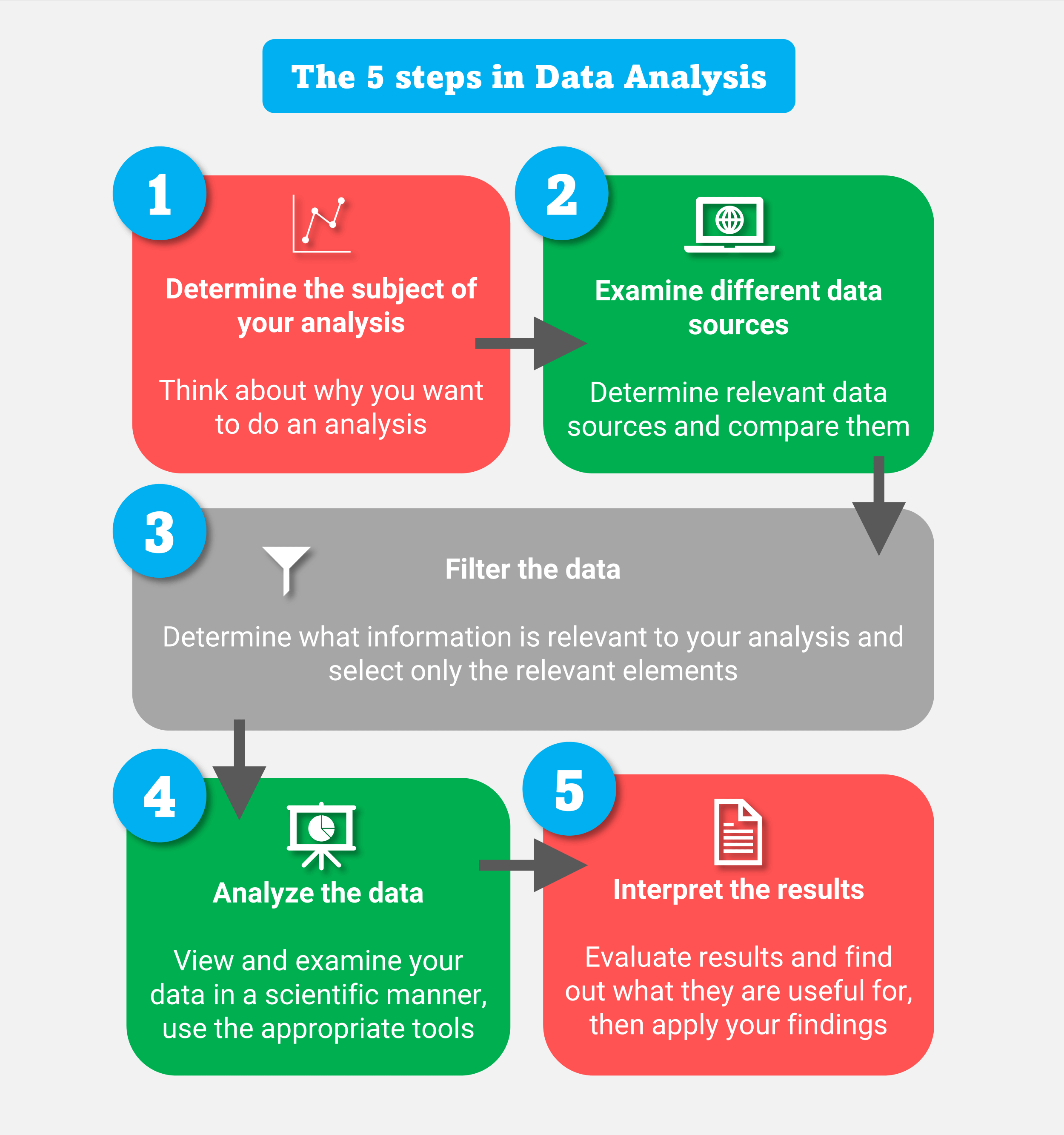
Data Analysis and Machine Learning
Discrete mathematics is used in data analysis and machine learning to develop algorithms for data mining, clustering, and classification. Discrete math helps us understand the structure and patterns in data, identify anomalies, and make predictions.
For instance, discrete math is used in natural language processing to develop algorithms for text analysis, sentiment analysis, and language modeling. Discrete math is also used in computer vision to develop algorithms for image recognition, object detection, and image segmentation.
Gallery of Discrete Math in Real-Life Applications





FAQs
What is discrete mathematics?
+Discrete mathematics is a branch of mathematics that deals with individual, distinct elements rather than continuous values.
How is discrete mathematics used in computer science?
+Discrete mathematics is used in computer science to develop efficient algorithms, ensure data integrity, and optimize system performance.
What are some real-life applications of discrete mathematics?
+Discrete mathematics has numerous real-life applications, including computer science, cryptography, network analysis, optimization, and data analysis.
We hope this article has provided you with a deeper understanding of the impact of discrete mathematics on real-life applications. From computer science and coding theory to network analysis and cryptography, discrete math plays a vital role in shaping the world we live in. We encourage you to explore the many applications of discrete mathematics and discover how it can be used to solve complex problems and optimize systems.
