Understanding algebra can be a daunting task, especially for beginners. However, with the right approach, it can be a fascinating and rewarding subject. Algebra is a fundamental branch of mathematics that deals with variables and their relationships. It has numerous applications in various fields, including science, engineering, economics, and computer science. In this article, we will explore the basics of algebra, its applications, and visualization techniques to help beginners master this essential math subject.

Why Learn Algebra?
Algebra is an essential tool for problem-solving and critical thinking. It helps you develop logical reasoning, analytical skills, and spatial awareness. By learning algebra, you can:
- Improve your problem-solving skills
- Enhance your analytical and critical thinking abilities
- Develop spatial awareness and visualization skills
- Prepare for advanced math and science courses
- Apply algebraic concepts to real-world problems
Algebraic Concepts for Beginners
Before diving into applications and visualization, let's cover some basic algebraic concepts:
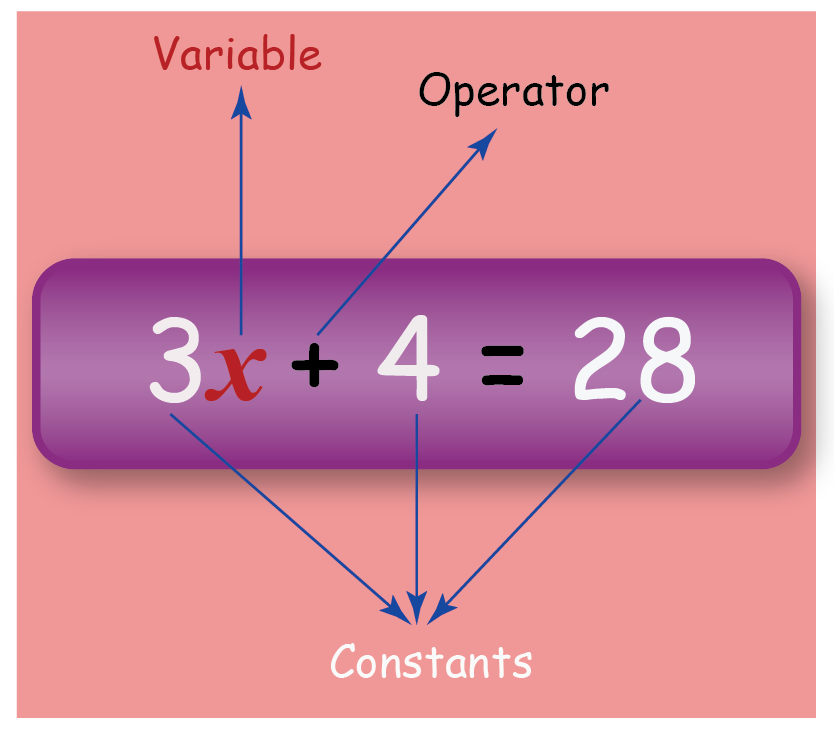
- Variables: Letters or symbols that represent unknown values
- Constants: Numbers that remain unchanged
- Coefficients: Numbers that multiply variables
- Expressions: Combinations of variables, constants, and coefficients
- Equations: Statements that express the equality of two expressions
Applications of Algebra
Algebra has numerous applications in various fields, including:
- Science: Algebra is used to describe the laws of physics, chemistry, and biology. It helps scientists model complex phenomena, make predictions, and analyze data.
- Engineering: Algebra is essential for designing and optimizing systems, structures, and processes. It helps engineers model real-world problems, make predictions, and analyze data.
- Economics: Algebra is used to model economic systems, understand the behavior of markets, and make predictions about economic trends.
- Computer Science: Algebra is used in computer programming, algorithm design, and data analysis.

Visualization Techniques for Algebra
Visualization is a powerful tool for understanding algebraic concepts. Here are some techniques to help you visualize algebra:
- Graphing: Use graphs to visualize relationships between variables
- Charts and Tables: Use charts and tables to organize and analyze data
- Geometric Shapes: Use geometric shapes to visualize algebraic expressions
- Animations: Use animations to visualize dynamic systems and processes
Tips for Mastering Algebra
Mastering algebra requires practice, patience, and persistence. Here are some tips to help you get started:
- Start with basics: Make sure you understand the basic concepts of algebra
- Practice regularly: Practice algebraic problems regularly to build your skills
- Use visualization techniques: Use visualization techniques to help you understand algebraic concepts
- Seek help: Seek help from teachers, tutors, or online resources when needed

Real-World Applications of Algebra
Algebra has numerous real-world applications, including:
- Predicting population growth: Algebra is used to model population growth and make predictions about future trends
- Designing roller coasters: Algebra is used to design roller coasters that are safe and fun
- Optimizing traffic flow: Algebra is used to optimize traffic flow and reduce congestion
- Modeling financial systems: Algebra is used to model financial systems and make predictions about market trends
Conclusion
Mastering algebra requires practice, patience, and persistence. By understanding the basics of algebra, using visualization techniques, and exploring real-world applications, you can develop a deep appreciation for this essential math subject. Remember to practice regularly, seek help when needed, and stay motivated. With time and effort, you can become proficient in algebra and unlock its many applications.

Gallery of Algebraic Concepts





FAQ
What is algebra?
+Algebra is a branch of mathematics that deals with variables and their relationships.
Why is algebra important?
+Algebra is essential for problem-solving, critical thinking, and spatial awareness.
How can I learn algebra?
+Start with the basics, practice regularly, use visualization techniques, and seek help when needed.
