Quadratic Functions Worksheet With Real-World Applications

Quick Links :

Quadratic functions are a fundamental concept in algebra, and they have numerous real-world applications in various fields such as physics, engineering, economics, and more. The ability to model and solve quadratic equations is essential for problem-solving in these fields. In this article, we will explore the concept of quadratic functions, their importance, and provide a comprehensive worksheet with real-world applications.

What are Quadratic Functions?

A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic function is:

f(x) = ax^2 + bx + c

where a, b, and c are constants, and a cannot be zero. Quadratic functions can be represented graphically as a parabola, which is a U-shaped curve that opens upwards or downwards.

Importance of Quadratic Functions

Quadratic functions have numerous real-world applications in various fields, including:

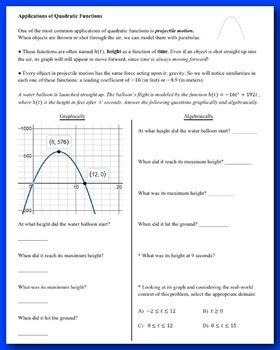
• Physics: Quadratic functions are used to model the motion of objects under the influence of gravity, such as the trajectory of a projectile.
• Engineering: Quadratic functions are used to design and optimize systems, such as bridges, buildings, and electronic circuits.
• Economics: Quadratic functions are used to model economic systems, such as the relationship between price and demand.
• Computer Science: Quadratic functions are used in algorithms for solving complex problems, such as sorting and searching.

Quadratic Functions Worksheet

Here is a comprehensive worksheet with real-world applications of quadratic functions:

Section 1: Solving Quadratic Equations

1. Solve the quadratic equation: x^2 + 5x + 6 = 0
2. Solve the quadratic equation: x^2 - 3x - 2 = 0
3. Solve the quadratic equation: x^2 + 2x - 6 = 0

Section 2: Graphing Quadratic Functions

1. Graph the quadratic function: f(x) = x^2 + 2x - 3
2. Graph the quadratic function: f(x) = x^2 - 4x - 2
3. Graph the quadratic function: f(x) = x^2 + x + 1

Section 3: Real-World Applications

1. A ball is thrown upwards from the ground with an initial velocity of 20 m/s. The height of the ball above the ground is given by the quadratic function: h(t) = -5t^2 + 20t + 1. Find the maximum height reached by the ball.
2. A company produces a product that has a quadratic cost function: C(x) = 2x^2 + 10x + 5, where x is the number of units produced. Find the minimum cost.
3. A bridge is designed to have a quadratic shape: y = -x^2 + 10x + 20, where y is the height above the ground and x is the distance from the center of the bridge. Find the maximum height of the bridge.

Section 4: Word Problems

1. A farmer has 100 meters of fencing to enclose a rectangular field. If the length of the field is x meters, find the maximum area of the field.
2. A company has a quadratic revenue function: R(x) = 2x^2 + 10x + 5, where x is the number of units sold. Find the maximum revenue.
3. A city has a quadratic population growth function: P(t) = 2t^2 + 10t + 1000, where t is the number of years since 2000. Find the maximum population growth rate.

Gallery of Quadratic Functions

Conclusion

In conclusion, quadratic functions are a fundamental concept in algebra with numerous real-world applications. The ability to model and solve quadratic equations is essential for problem-solving in various fields. The worksheet provided in this article includes a comprehensive set of problems with real-world applications, including graphing quadratic functions, solving quadratic equations, and word problems. We hope this article has been helpful in illustrating the importance of quadratic functions and providing a valuable resource for learning.

FAQ Section