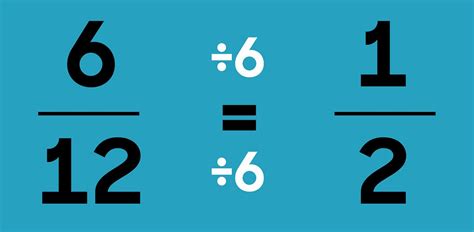6 Divided By 2 Simplified

Quick Links :

The Benefits of Simplifying Fractions

Simplifying fractions is a fundamental concept in mathematics that involves reducing a fraction to its simplest form. In this article, we will explore the benefits of simplifying fractions, with a focus on the specific case of 6 divided by 2.

Why Simplify Fractions?

Simplifying fractions is an essential skill in mathematics, as it helps to:

• Reduce confusion: Complex fractions can be confusing and difficult to work with. Simplifying fractions makes it easier to understand and manipulate them.
• Improve accuracy: Simplifying fractions reduces the risk of errors and ensures that calculations are accurate.
• Enhance problem-solving: Simplifying fractions enables students to solve problems more efficiently and effectively.

How to Simplify Fractions

Simplifying fractions involves dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.

Example: 6 Divided by 2

To simplify the fraction 6/2, we need to find the GCD of 6 and 2. The GCD of 6 and 2 is 2.

Therefore, we can simplify the fraction by dividing both the numerator and denominator by 2:

6 ÷ 2 = 3 2 ÷ 2 = 1

So, the simplified fraction is 3/1.

Benefits of Simplifying 6 Divided by 2

Simplifying the fraction 6/2 has several benefits, including:

• Reduced complexity: The simplified fraction 3/1 is easier to understand and work with than the original fraction 6/2.
• Improved accuracy: Simplifying the fraction reduces the risk of errors and ensures that calculations are accurate.
• Enhanced problem-solving: The simplified fraction enables students to solve problems more efficiently and effectively.

Real-World Applications

Simplifying fractions has numerous real-world applications, including:

• Cooking: Simplifying fractions is essential in cooking, where recipes often involve fractions of ingredients.
• Finance: Simplifying fractions is crucial in finance, where interest rates and investment returns are often expressed as fractions.
• Science: Simplifying fractions is important in science, where measurements and calculations often involve fractions.

Conclusion

Simplifying fractions is a fundamental concept in mathematics that has numerous benefits and real-world applications. By simplifying fractions, students can reduce complexity, improve accuracy, and enhance problem-solving skills. The specific case of 6 divided by 2 demonstrates the importance of simplifying fractions and highlights the benefits of reducing fractions to their simplest form.