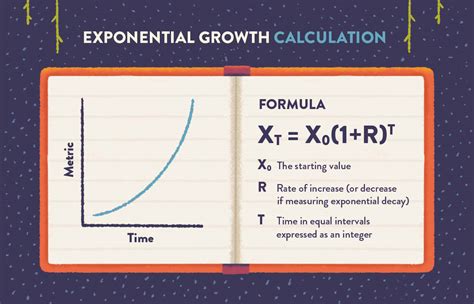
Exponential equations are a fundamental concept in mathematics, and they have numerous practical applications in various fields. These equations describe situations where a quantity changes at a rate proportional to its current value, resulting in rapid growth or decay. Here are six ways exponential equations are used in real life, showcasing their significance and impact.

1. Population Growth and Epidemics
Exponential equations are used to model population growth, where the rate of increase is proportional to the current population size. This concept is essential in understanding the spread of diseases, as it helps epidemiologists predict the number of infected individuals and the rate at which the disease will spread.
For instance, the SIR model, which describes the spread of infectious diseases, relies heavily on exponential equations. The model categorizes individuals into three groups: Susceptible (S), Infected (I), and Recovered (R). The rate of change in each group is described by exponential equations, allowing researchers to forecast the progression of the disease.
2. Financial Investments and Compound Interest
Compound interest is a fundamental concept in finance, where the interest earned on an investment is reinvested, resulting in exponential growth. Exponential equations are used to calculate the future value of an investment, taking into account the principal amount, interest rate, and compounding frequency.
For example, if you deposit $1,000 into a savings account with a 5% annual interest rate compounded monthly, the future value of the investment can be calculated using an exponential equation. This helps investors understand the potential returns on their investments and make informed decisions.
3. Chemical Reactions and Half-Life
Exponential equations are used to describe the decay of radioactive substances, where the rate of decay is proportional to the current amount of the substance. This concept is crucial in understanding the half-life of radioactive materials, which is the time it takes for the substance to decay by half.
Chemical reactions also involve exponential equations, where the rate of reaction is described by the Arrhenius equation. This equation takes into account the activation energy, temperature, and concentration of reactants to predict the rate of reaction.
4. Electrical Circuits and Resistance
Exponential equations are used to analyze electrical circuits, where the voltage and current are related by exponential equations. The RC circuit, which consists of a resistor and capacitor, is a classic example of an exponential equation in action.
When a voltage is applied to the circuit, the current flows through the resistor and charges the capacitor. The voltage across the capacitor is described by an exponential equation, which helps engineers design and analyze electrical circuits.
5. Computer Science and Algorithm Analysis
Exponential equations are used to analyze the time complexity of algorithms, which is a measure of how long an algorithm takes to complete. The time complexity is often described by exponential equations, where the running time grows exponentially with the size of the input.
For example, the Fibonacci sequence is a classic example of an exponential equation in computer science. The sequence is generated recursively, and the running time of the algorithm grows exponentially with the size of the input.
6. Biological Systems and Growth Models
Exponential equations are used to model the growth of biological systems, such as populations of bacteria, cells, or organisms. The logistic growth model, which describes the growth of a population in a limited environment, relies heavily on exponential equations.
The model takes into account the carrying capacity of the environment, the growth rate, and the initial population size to predict the future population size. This concept is essential in understanding the dynamics of biological systems and predicting the outcomes of various scenarios.

Gallery of Exponential Equations in Real Life:






FAQ:
What is an exponential equation?
+An exponential equation is a mathematical equation that describes a situation where a quantity changes at a rate proportional to its current value.
How are exponential equations used in real life?
+Exponential equations are used in various fields, including population growth, financial investments, chemical reactions, electrical circuits, computer science, and biological systems.
What is the significance of exponential equations in finance?
+Exponential equations are used to calculate the future value of an investment, taking into account the principal amount, interest rate, and compounding frequency.
We hope this article has provided you with a deeper understanding of exponential equations and their applications in real life. These equations play a crucial role in modeling and analyzing various phenomena, and their significance extends across multiple disciplines. Whether you're a student, researcher, or professional, understanding exponential equations can help you make informed decisions and tackle complex problems in your field.