The concept of fractions is a fundamental aspect of mathematics, and understanding how to simplify them is crucial for problem-solving and critical thinking. In this article, we will delve into the world of fractions and explore what it means to simplify them, using the example of 33 as a simplified fraction.
What are Fractions?
Fractions are a way of expressing a part of a whole as a ratio of two numbers. They consist of a numerator (the top number) and a denominator (the bottom number), separated by a line. Fractions can be used to represent a wide range of mathematical concepts, from measurements and proportions to algebra and geometry.
Understanding Simplifying Fractions
Simplifying fractions is the process of reducing a fraction to its simplest form by dividing both the numerator and the denominator by the greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.

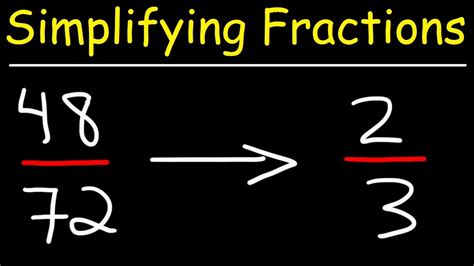
For example, let's take the fraction 12/16. To simplify this fraction, we need to find the GCD of 12 and 16, which is 4. By dividing both the numerator and the denominator by 4, we get the simplified fraction 3/4.
33 as a Simplified Fraction
Now, let's consider the fraction 33. At first glance, it may seem like a simple fraction, but is it in its simplest form?
To determine if 33 is a simplified fraction, we need to find the GCD of 33 and 1 (since the denominator is 1). The GCD of 33 and 1 is 1, which means that 33 is indeed a simplified fraction.
However, we can take it a step further. Since the numerator is 33, we can express it as a product of its prime factors: 3 × 11. But what about the denominator? Can we simplify it further?
In this case, the answer is no. The denominator 1 is already in its simplest form, and we cannot simplify it further.

So, what does this mean? It means that 33 is indeed a simplified fraction, but it's not a fraction in the classical sense. Instead, it's a whole number that can be expressed as a fraction with a denominator of 1.
Real-World Applications of Simplifying Fractions
Simplifying fractions may seem like a theoretical concept, but it has many real-world applications. Here are a few examples:
- Cooking: When following a recipe, you may need to simplify fractions to get the right proportions of ingredients. For example, if a recipe calls for 1/4 cup of sugar, but you only have a 1/8 cup measuring cup, you can simplify the fraction to get the right amount.
- Finance: In finance, simplifying fractions is crucial for calculating interest rates, investment returns, and other financial metrics.
- Science: In science, fractions are used to express ratios and proportions of different quantities. Simplifying fractions is essential for making accurate calculations and predictions.

In conclusion, simplifying fractions is an essential concept in mathematics, and understanding how to simplify them is crucial for problem-solving and critical thinking. The example of 33 as a simplified fraction shows that even seemingly simple fractions can have complex underlying structures. By mastering the art of simplifying fractions, you'll be able to tackle a wide range of mathematical problems with confidence.
Gallery of Simplifying Fractions






What is a simplified fraction?
+A simplified fraction is a fraction that has been reduced to its simplest form by dividing both the numerator and the denominator by the greatest common divisor (GCD).
Why is simplifying fractions important?
+Simplifying fractions is important because it allows us to express ratios and proportions in their simplest form, making it easier to perform mathematical operations and make calculations.
Can all fractions be simplified?
+No, not all fractions can be simplified. Some fractions, like 33, are already in their simplest form.
We hope this article has helped you understand the concept of simplifying fractions and how to apply it in real-world situations. If you have any further questions or need help with a specific problem, feel free to ask in the comments below!