To convert a fraction to a percentage, we need to divide the numerator (1) by the denominator (7) and multiply by 100.
1 ÷ 7 = 0.1429 ( rounded to 4 decimal places)
Multiply by 100:
0.1429 × 100 = 14.29%
So, 1 in 7 as a percentage is approximately 14.29%.
Understanding Fractions and Percentages
Fractions and percentages are used to represent part of a whole. A fraction is a way to show a part of a whole as a ratio of two numbers, while a percentage is a way to show a part of a whole as a proportion of 100.
In the case of 1 in 7, the fraction can be represented as 1/7. To convert this fraction to a percentage, we can use the formula:
Percentage = (numerator ÷ denominator) × 100
Real-World Applications of Fractions and Percentages
Fractions and percentages are used in many real-world applications, such as:
- Cooking: Recipes often use fractions and percentages to measure ingredients.
- Finance: Interest rates and investment returns are often expressed as percentages.
- Statistics: Percentages are used to represent proportions of data in statistical analysis.

Converting Fractions to Percentages
To convert a fraction to a percentage, follow these steps:
- Divide the numerator by the denominator.
- Multiply the result by 100.
For example, to convert the fraction 3/4 to a percentage:
3 ÷ 4 = 0.75 0.75 × 100 = 75%
So, the fraction 3/4 is equal to 75%.
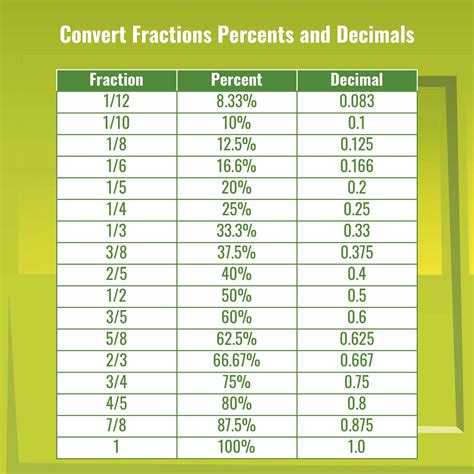
Common Fraction to Percentage Conversions
Here are some common fraction to percentage conversions:
- 1/2 = 50%
- 1/4 = 25%
- 3/4 = 75%
- 2/3 = 66.67%

Percentage Increase and Decrease
Percentages can also be used to show an increase or decrease in a value. For example, if a price increases by 10%, it means that the new price is 110% of the original price.
To calculate a percentage increase or decrease, use the following formulas:
- Percentage increase = (new value - original value) ÷ original value × 100
- Percentage decrease = (original value - new value) ÷ original value × 100
For example, if a price increases from $100 to $120, the percentage increase is:
($120 - $100) ÷ $100 × 100 = 20%
So, the price has increased by 20%.

Real-World Applications of Percentage Increase and Decrease
Percentage increase and decrease are used in many real-world applications, such as:
- Finance: Interest rates and investment returns are often expressed as percentage increases or decreases.
- Business: Companies use percentage increases and decreases to measure changes in sales, revenue, and profits.
- Statistics: Percentages are used to represent changes in data over time.
Gallery of Fractions and Percentages:





FAQ:
What is the formula to convert a fraction to a percentage?
+The formula to convert a fraction to a percentage is: (numerator ÷ denominator) × 100.
What is the difference between a percentage increase and a percentage decrease?
+A percentage increase is a change in a value that results in a higher value, while a percentage decrease is a change in a value that results in a lower value.
What are some common fraction to percentage conversions?
+Some common fraction to percentage conversions include: 1/2 = 50%, 1/4 = 25%, 3/4 = 75%, and 2/3 = 66.67%.
We hope you found this article helpful in understanding fractions and percentages. Whether you're a student, a business owner, or simply someone who wants to improve their math skills, fractions and percentages are essential concepts to grasp.