Triangles are a fundamental concept in geometry, and their properties have far-reaching implications in various fields. One of the most significant aspects of triangles is similarity, which refers to the relationship between two triangles that have the same shape but not necessarily the same size. In this article, we will explore five ways triangle similarity impacts real-world applications.
Understanding Triangle Similarity
Before diving into the applications of triangle similarity, it's essential to understand what it means for two triangles to be similar. Two triangles are similar if their corresponding angles are congruent, and their corresponding sides are proportional. This means that if two triangles have the same shape, but one is larger or smaller than the other, they are similar.

Application 1: Architecture and Building Design
Triangle similarity plays a crucial role in architecture and building design. When designing a building, architects often use similar triangles to ensure that the structure is proportional and aesthetically pleasing. For example, the shape of a roof or a bridge can be designed using similar triangles to create a sense of balance and harmony.

Benefits of Similar Triangles in Architecture
Similar triangles offer several benefits in architecture, including:
- Aesthetics: Similar triangles can create a sense of balance and harmony in a building's design.
- Proportionality: Similar triangles ensure that the different parts of a building are proportional to each other.
- Structural integrity: Similar triangles can help distribute stress and weight evenly throughout a building, making it more stable.
Application 2: Physics and Engineering
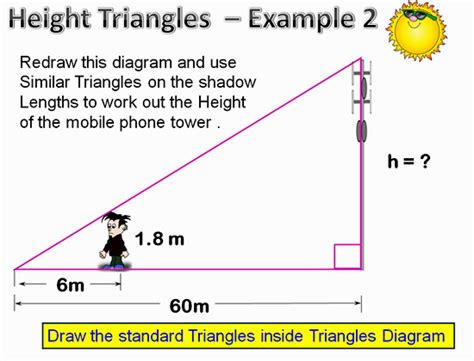
Triangle similarity has numerous applications in physics and engineering. One of the most significant applications is in the calculation of distances and heights. By using similar triangles, physicists and engineers can calculate the height of a building or the distance to a distant object.

How Similar Triangles are Used in Physics and Engineering
Similar triangles are used in physics and engineering in the following ways:
- Calculating distances: Similar triangles can be used to calculate the distance to a distant object by measuring the angle of elevation and the height of the object.
- Calculating heights: Similar triangles can be used to calculate the height of a building or a mountain by measuring the angle of elevation and the distance to the object.
Application 3: Computer Graphics and Game Development
Triangle similarity has numerous applications in computer graphics and game development. One of the most significant applications is in the creation of 3D models and animations. By using similar triangles, game developers can create realistic and detailed 3D models.

Benefits of Similar Triangles in Computer Graphics and Game Development
Similar triangles offer several benefits in computer graphics and game development, including:
- Realism: Similar triangles can create realistic and detailed 3D models.
- Efficiency: Similar triangles can reduce the number of polygons required to create a 3D model, making it more efficient to render.
Application 4: Navigation and Surveying
Triangle similarity has numerous applications in navigation and surveying. One of the most significant applications is in the calculation of distances and angles. By using similar triangles, navigators and surveyors can calculate the distance to a distant object or the angle between two points.

How Similar Triangles are Used in Navigation and Surveying
Similar triangles are used in navigation and surveying in the following ways:
- Calculating distances: Similar triangles can be used to calculate the distance to a distant object by measuring the angle of elevation and the height of the object.
- Calculating angles: Similar triangles can be used to calculate the angle between two points by measuring the angle of elevation and the distance to the object.
Application 5: Art and Design
Triangle similarity has numerous applications in art and design. One of the most significant applications is in the creation of patterns and designs. By using similar triangles, artists and designers can create intricate and detailed patterns.

Benefits of Similar Triangles in Art and Design
Similar triangles offer several benefits in art and design, including:
- Intricacy: Similar triangles can create intricate and detailed patterns.
- Aesthetics: Similar triangles can create a sense of balance and harmony in a design.






What is triangle similarity?
+Triangle similarity refers to the relationship between two triangles that have the same shape but not necessarily the same size.
What are the benefits of similar triangles in architecture?
+Similar triangles offer several benefits in architecture, including aesthetics, proportionality, and structural integrity.
How are similar triangles used in computer graphics and game development?
+Similar triangles are used in computer graphics and game development to create realistic and detailed 3D models.
In conclusion, triangle similarity has numerous applications in various fields, including architecture, physics, engineering, computer graphics, game development, navigation, surveying, art, and design. By understanding the concept of triangle similarity, we can create more efficient, effective, and aesthetically pleasing designs and solutions.