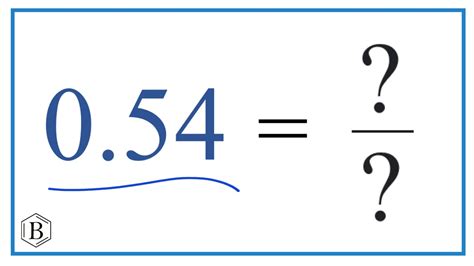The importance of converting decimals to fractions cannot be overstated. Decimals are a convenient way to represent numbers, but fractions offer a more precise and nuanced understanding of mathematical relationships. In this article, we will explore the process of converting 0.54 to a fraction and simplify it.
Understanding the Basics of Converting Decimals to Fractions
Converting decimals to fractions is a fundamental concept in mathematics. It involves expressing a decimal number as a ratio of two integers, i.e., a fraction. To convert a decimal to a fraction, we need to understand the concept of place value.
Converting 0.54 to a Fraction
To convert 0.54 to a fraction, we need to express it as a ratio of two integers. Since 0.54 is a decimal number with two digits after the decimal point, we can express it as:
0.54 = 54/100
Simplifying the Fraction
Now that we have expressed 0.54 as a fraction, we need to simplify it. Simplifying a fraction involves dividing both the numerator and the denominator by the greatest common divisor (GCD) of the two numbers.
In this case, the GCD of 54 and 100 is 2. Therefore, we can simplify the fraction as follows:
54 ÷ 2 = 27 100 ÷ 2 = 50
So, the simplified fraction is:
27/50
Image: Converting Decimals to Fractions

Benefits of Simplifying Fractions
Simplifying fractions is an essential concept in mathematics. It helps us to express fractions in their simplest form, making it easier to work with them. Simplifying fractions also helps us to identify equivalent fractions, which is crucial in various mathematical operations such as addition, subtraction, multiplication, and division.
Real-World Applications of Simplifying Fractions
Simplifying fractions has numerous real-world applications. For example, in cooking, fractions are used to represent ingredients and measurements. Simplifying fractions helps cooks to ensure that they use the correct proportions of ingredients, which is crucial in achieving the desired flavor and texture.
Image: Real-World Applications of Simplifying Fractions

Common Mistakes to Avoid When Simplifying Fractions
When simplifying fractions, there are several common mistakes to avoid. One of the most common mistakes is dividing both the numerator and the denominator by a number that is not the GCD. This can result in an incorrect simplification of the fraction.
Another common mistake is failing to check if the fraction can be simplified further. For example, if we simplify a fraction and the resulting fraction has a numerator and denominator that are both even, we can simplify it further by dividing both numbers by 2.
Conclusion: Mastering the Art of Simplifying Fractions
In conclusion, simplifying fractions is a fundamental concept in mathematics. It involves expressing a fraction in its simplest form, making it easier to work with. By mastering the art of simplifying fractions, we can improve our mathematical skills and develop a deeper understanding of mathematical relationships.
Gallery of Simplifying Fractions





FAQ
What is the purpose of simplifying fractions?
+The purpose of simplifying fractions is to express a fraction in its simplest form, making it easier to work with.
How do I simplify a fraction?
+To simplify a fraction, divide both the numerator and the denominator by the greatest common divisor (GCD) of the two numbers.
What are the benefits of simplifying fractions?
+The benefits of simplifying fractions include improved mathematical skills, deeper understanding of mathematical relationships, and easier working with fractions.