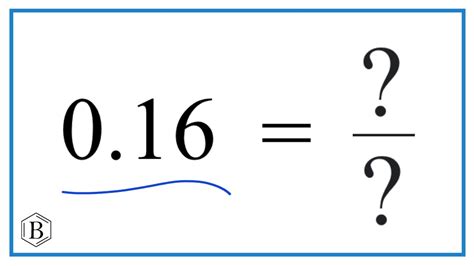Repeating decimals have always been a fascinating topic in mathematics. One such repeating decimal that often raises curiosity is 0.16 repeating. In this article, we will explore the concept of 0.16 repeating as a fraction and provide a simplified explanation.
What is a Repeating Decimal?
Before we dive into 0.16 repeating, let's understand what a repeating decimal is. A repeating decimal is a decimal representation of a number where a finite block of digits repeats indefinitely. For example, 0.333... is a repeating decimal because the digit 3 repeats indefinitely.

Converting 0.16 Repeating to a Fraction
To convert 0.16 repeating to a fraction, we can use algebraic manipulation. Let's denote 0.16 repeating as x.
0.16 repeating = 0.161616...
We can multiply x by 100 to shift the decimal point two places to the right.
100x = 16.161616...
Now, subtract x from 100x to eliminate the repeating part.
100x - x = 16.161616... - 0.161616...
This simplifies to:
99x = 16
Now, divide both sides by 99 to solve for x.
x = 16/99
Therefore, 0.16 repeating as a fraction is 16/99.

Why is 16/99 Important?
The fraction 16/99 may seem insignificant, but it has real-world applications. For instance, in music theory, the ratio 16:99 is used to calculate the frequency of notes. In addition, this fraction can be used in mathematical modeling, such as population growth and chemical reactions.
Practical Applications of 16/99
- Music Theory: The ratio 16:99 is used to calculate the frequency of notes in music.
- Mathematical Modeling: This fraction can be used to model population growth, chemical reactions, and other real-world phenomena.
- Science: The ratio 16:99 appears in scientific calculations, such as determining the volume of a cylinder.

Conclusion and Next Steps
In conclusion, 0.16 repeating as a fraction is a fascinating mathematical concept with real-world applications. By understanding how to convert repeating decimals to fractions, we can unlock a deeper understanding of mathematical modeling and scientific calculations.
If you're interested in learning more about repeating decimals and their applications, we encourage you to explore further. The world of mathematics is full of intriguing concepts waiting to be discovered.






What is a repeating decimal?
+A repeating decimal is a decimal representation of a number where a finite block of digits repeats indefinitely.
How do you convert a repeating decimal to a fraction?
+To convert a repeating decimal to a fraction, you can use algebraic manipulation, such as multiplying the decimal by a power of 10 and then subtracting the original decimal.
What are some real-world applications of the fraction 16/99?
+The fraction 16/99 has real-world applications in music theory, mathematical modeling, and scientific calculations.